How to check if two line segments intersect

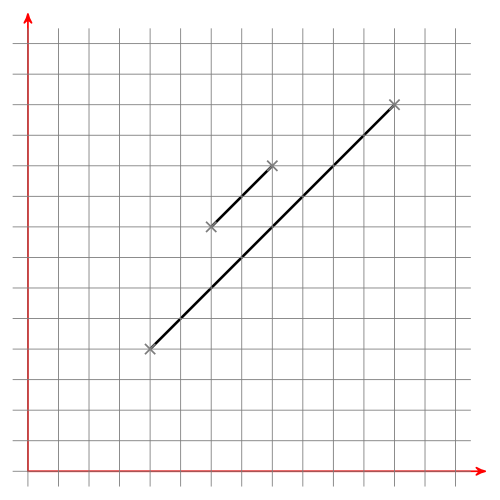
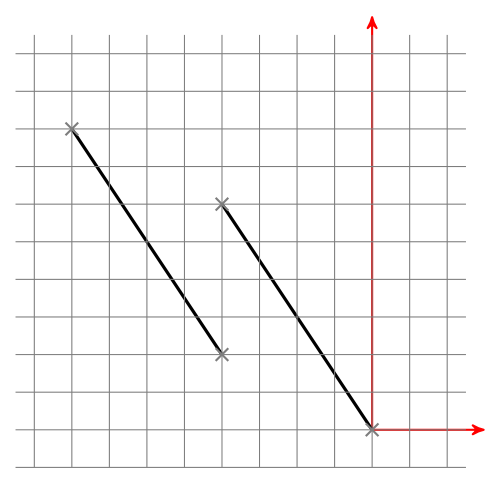
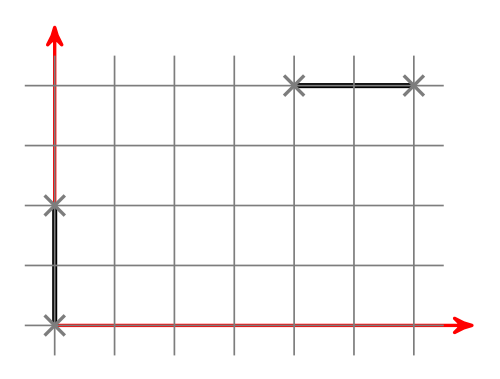
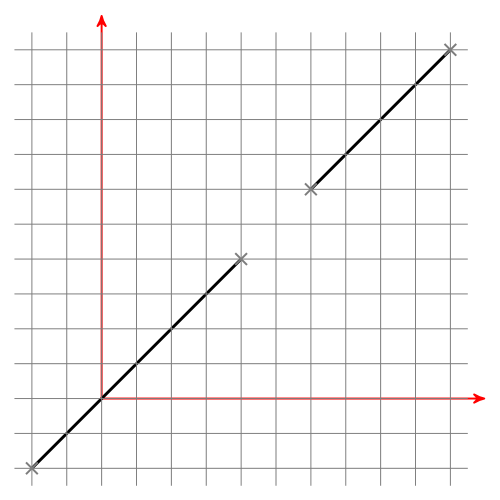
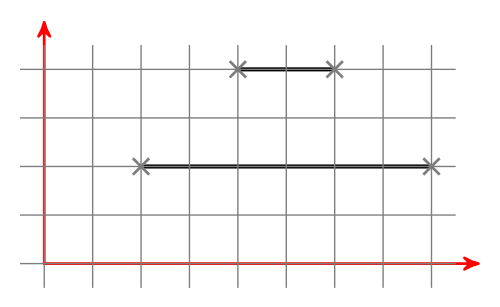
You have to line segments and you want to know if they intersect. I'll give you an algorithm how to do it.

Test cases

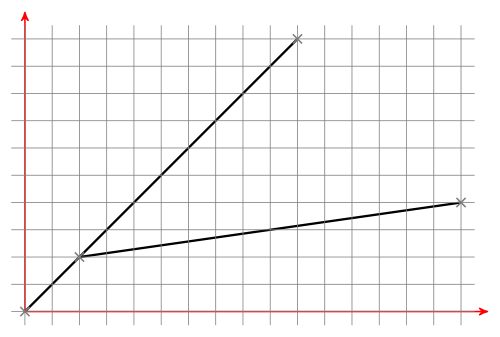
First of all, we should think about how lines can be arranged:

Testcase T1
Testcase T2
Testcase T3
Testcase T4
Testcase T5
Testcase T6
Testcase F1
Testcase F2
Testcase F3
Testcase F4
Testcase F5
Testcase F6
Testcase F7
Testcase F8

Bounding boxes

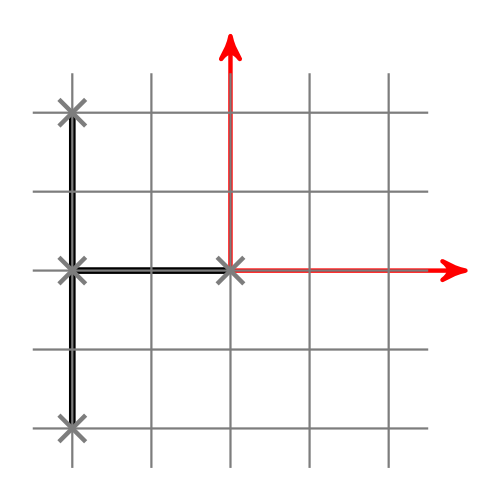
You can draw boxes around line segments such that the edges of the boxes are in parallel to the coordinate axes:

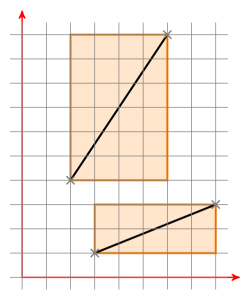
With this image in mind, it is obvious that the bounding boxes need to intersect if the lines should intersect. At this point you have to make a decision: If the endpoint of one line is on the other line, is this an intersection? I think so. If two lines have at least one point in common, they intersect. If two bounding boxes have at least one point in common, they intersect.

It is much easier to check if two bounding boxes intersect. It's simply:

/**
 * Check if bounding boxes do intersect. If one bounding box
 * touches the other, they do intersect.
 * @param a first bounding box
 * @param b second bounding box
 * @return <code>true</code> if they intersect,
 *         <code>false</code> otherwise.
 */
public boolean doBoundingBoxesIntersect(Point[] a, Point[] b) {
    return a[0].x <= b[1].x
        && a[1].x >= b[0].x
        && a[0].y <= b[1].y
        && a[1].y >= b[0].y;
}

If you have difficulties to understand why this works, take a look at this great animation for this formula.

The algorithm

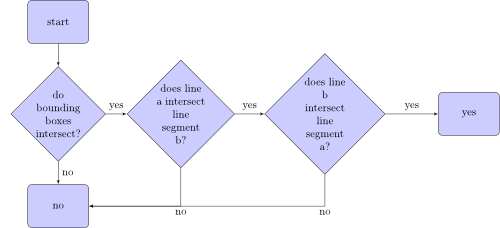
Flowchart how to check if two lines intersect

Looks quite simple, doesn't it?

Cross product

Well, you might notice that you need to check if one line intersects with a given line segment. To check this, you have to understand one cool idea:

You can definie a cross product for points:

\begin{align} \times_P&: Point \times Point \rightarrow \mathbb{R}\\ \times_P(a, b) &:= a.x \cdot b.y - b.x \cdot a.y; \end{align}

This cross product has one nice characteristics:

$a \times_P b = 0 \Leftrightarrow a$ and $b$ are on one line through origin

You can verify this. If you take two points on a line through origin, they have the same slope $\frac{\Delta y}{\Delta x}$:

$$ \begin{align} 0 &= a \times_P b\\ \Leftrightarrow 0 &= a.x \cdot b.y - b.x \cdot a.y\\ \Leftrightarrow b.x \cdot a.y &= a.x \cdot b.y\\ \Leftrightarrow \frac{a.y}{a.x} &= \frac{b.y}{b.x} \end{align} $$

Ok, now you can check if a point is on a line:

/**
 * Checks if a Point is on a line
 * @param a line (interpreted as line, although given as line
 *                segment)
 * @param b point
 * @return <code>true</code> if point is on line, otherwise
 *         <code>false</code>
 */
public boolean isPointOnLine(LineSegment a, Point b) {
    // Move the image, so that a.first is on (0|0)
    LineSegment aTmp = new LineSegment(new Point(0, 0), new Point(
            a.second.x - a.first.x, a.second.y - a.first.y));
    Point bTmp = new Point(b.x - a.first.x, b.y - a.first.y);
    double r = crossProduct(aTmp.second, bTmp);
    return Math.abs(r) < EPSILON;
}

The second cool characteristic of the cross product is that it can be used to determine if a point b is left or right of the line through the origin and a point a:

/**
 * Checks if a point is right of a line. If the point is on the
 * line, it is not right of the line.
 * @param a line segment interpreted as a line
 * @param b the point
 * @return <code>true</code> if the point is right of the line,
 *         <code>false</code> otherwise
 */
public boolean isPointRightOfLine(LineSegment a, Point b) {
    // Move the image, so that a.first is on (0|0)
    LineSegment aTmp = new LineSegment(new Point(0, 0), new Point(
            a.second.x - a.first.x, a.second.y - a.first.y));
    Point bTmp = new Point(b.x - a.first.x, b.y - a.first.y);
    return crossProduct(aTmp.second, bTmp) < 0;
}

When we have one line $a$ through the origin and one line segment $b$, you can check if $b$ crosses $a$ by checking if the end points of $b$ are on different sides of $a$:

/**
 * Check if line segment first touches or crosses the line that is
 * defined by line segment second.
 *
 * @param first line segment interpreted as line
 * @param second line segment
 * @return <code>true</code> if line segment first touches or
 *                           crosses line second,
 *         <code>false</code> otherwise.
 */
public boolean lineSegmentTouchesOrCrossesLine(LineSegment a,
        LineSegment b) {
    return isPointOnLine(a, b.first)
            || isPointOnLine(a, b.second)
            || (isPointRightOfLine(a, b.first) ^
                isPointRightOfLine(a, b.second));
}

Now you have everything you need:

/**
 * Check if line segments intersect
 * @param a first line segment
 * @param b second line segment
 * @return <code>true</code> if lines do intersect,
 *         <code>false</code> otherwise
 */
public boolean doLinesIntersect(LineSegment a, LineSegment b) {
    Point[] box1 = a.getBoundingBox();
    Point[] box2 = b.getBoundingBox();
    return doBoundingBoxesIntersect(box1, box2)
            && lineSegmentTouchesOrCrossesLine(a, b)
            && lineSegmentTouchesOrCrossesLine(b, a);
}

By the way, testcase F5 is the only reason why you need doBoundingBoxesIntersect(box1, box2). All other tests still pass if you remove this function.

Where do two line segments intersect?

When you know that two line segments intersect, you can also calculate the intersection. The intersection could be a line or only a point.

I did this with JavaScript:

This is the code that checks for line segments:

/** You know that lines a and b have an intersection and now you
    want to get it!
*/
function getIntersection(a, b) {
    /* the intersection [(x1,y1), (x2, y2)]
       it might be a line or a single point. If it is a line,
       then x1 = x2 and y1 = y2.  */
    var x1, y1, x2, y2;

   if (a["first"]["x"] == a["second"]["x"]) {
        // Case (A)
        // As a is a perfect vertical line, it cannot be represented
        // nicely in a mathematical way. But we directly know that
        //
        x1 = a["first"]["x"];
        x2 = x1;
        if (b["first"]["x"] == b["second"]["x"]) {
            // Case (AA): all x are the same!
            // Normalize
            if(a["first"]["y"] > a["second"]["y"]) {
                a = {"first": a["second"], "second": a["first"]};
            }
            if(b["first"]["y"] > b["second"]["y"]) {
                b = {"first": b["second"], "second": b["first"]};
            }
            if(a["first"]["y"] > b["first"]["y"]) {
                var tmp = a;
                a = b;
                b = tmp;
            }

            // Now we know that the y-value of a["first"] is the
            // lowest of all 4 y values
            // this means, we are either in case (AAA):
            //   a: x--------------x
            //   b:    x---------------x
            // or in case (AAB)
            //   a: x--------------x
            //   b:    x-------x
            // in both cases:
            // get the relavant y intervall
            y1 = b["first"]["y"];
            y2 = Math.min(a["second"]["y"], b["second"]["y"]);
        } else {
            // Case (AB)
            // we can mathematically represent line b as
            //     y = m*x + t <=> t = y - m*x
            // m = (y1-y2)/(x1-x2)
            var m, t;
            m = (b["first"]["y"] - b["second"]["y"])/
                (b["first"]["x"] - b["second"]["x"]);
            t = b["first"]["y"] - m*b["first"]["x"];
            y1 = m*x1 + t;
            y2 = y1
        }
    } else if (b["first"]["x"] == b["second"]["x"]) {
        // Case (B)
        // essentially the same as Case (AB), but with
        // a and b switched
        x1 = b["first"]["x"];
        x2 = x1;

        var tmp = a;
        a = b;
        b = tmp;

        var m, t;
        m = (b["first"]["y"] - b["second"]["y"])/
            (b["first"]["x"] - b["second"]["x"]);
        t = b["first"]["y"] - m*b["first"]["x"];
        y1 = m*x1 + t;
        y2 = y1
    } else {
        // Case (C)
        // Both lines can be represented mathematically
        var ma, mb, ta, tb;
        ma = (a["first"]["y"] - a["second"]["y"])/
             (a["first"]["x"] - a["second"]["x"]);
        mb = (b["first"]["y"] - b["second"]["y"])/
             (b["first"]["x"] - b["second"]["x"]);
        ta = a["first"]["y"] - ma*a["first"]["x"];
        tb = b["first"]["y"] - mb*b["first"]["x"];
        if (ma == mb) {
            // Case (CA)
            // both lines are in parallel. As we know that they
            // intersect, the intersection could be a line
            // when we rotated this, it would be the same situation
            // as in case (AA)

            // Normalize
            if(a["first"]["x"] > a["second"]["x"]) {
                a = {"first": a["second"], "second": a["first"]};
            }
            if(b["first"]["x"] > b["second"]["x"]) {
                b = {"first": b["second"], "second": b["first"]};
            }
            if(a["first"]["x"] > b["first"]["x"]) {
                var tmp = a;
                a = b;
                b = tmp;
            }

            // get the relavant x intervall
            x1 = b["first"]["x"];
            x2 = Math.min(a["second"]["x"], b["second"]["x"]);
            y1 = ma*x1+ta;
            y2 = ma*x2+ta;
        } else {
            // Case (CB): only a point as intersection:
            // y = ma*x+ta
            // y = mb*x+tb
            // ma*x + ta = mb*x + tb
            // (ma-mb)*x = tb - ta
            // x = (tb - ta)/(ma-mb)
            x1 = (tb-ta)/(ma-mb);
            y1 = ma*x1+ta;
            x2 = x1;
            y2 = y1;
        }
    }

    return {"first": {"x":x1, "y":y1}, "second": {"x":x2, "y":y2}};
}

TL;DR

The complete, tested code is on GitHub. Here is the most important part:

public class Geometry {

    public static final double EPSILON = 0.000001;

    /**
     * Calculate the cross product of two points.
     * @param a first point
     * @param b second point
     * @return the value of the cross product
     */
    public static double crossProduct(Point a, Point b) {
        return a.x * b.y - b.x * a.y;
    }

    /**
     * Check if bounding boxes do intersect. If one bounding box
     * touches the other, they do intersect.
     * @param a first bounding box
     * @param b second bounding box
     * @return <code>true</code> if they intersect,
     *         <code>false</code> otherwise.
     */
    public static boolean doBoundingBoxesIntersect(Point[] a, Point[] b) {
        return a[0].x <= b[1].x && a[1].x >= b[0].x && a[0].y <= b[1].y
                && a[1].y >= b[0].y;
    }

    /**
     * Checks if a Point is on a line
     * @param a line (interpreted as line, although given as line
     *                segment)
     * @param b point
     * @return <code>true</code> if point is on line, otherwise
     *         <code>false</code>
     */
    public static boolean isPointOnLine(LineSegment a, Point b) {
        // Move the image, so that a.first is on (0|0)
        LineSegment aTmp = new LineSegment(new Point(0, 0), new Point(
                a.second.x - a.first.x, a.second.y - a.first.y));
        Point bTmp = new Point(b.x - a.first.x, b.y - a.first.y);
        double r = crossProduct(aTmp.second, bTmp);
        return Math.abs(r) < EPSILON;
    }

    /**
     * Checks if a point is right of a line. If the point is on the
     * line, it is not right of the line.
     * @param a line segment interpreted as a line
     * @param b the point
     * @return <code>true</code> if the point is right of the line,
     *         <code>false</code> otherwise
     */
    public static boolean isPointRightOfLine(LineSegment a, Point b) {
        // Move the image, so that a.first is on (0|0)
        LineSegment aTmp = new LineSegment(new Point(0, 0), new Point(
                a.second.x - a.first.x, a.second.y - a.first.y));
        Point bTmp = new Point(b.x - a.first.x, b.y - a.first.y);
        return crossProduct(aTmp.second, bTmp) < 0;
    }

    /**
     * Check if line segment first touches or crosses the line that is
     * defined by line segment second.
     *
     * @param first line segment interpreted as line
     * @param second line segment
     * @return <code>true</code> if line segment first touches or
     *                           crosses line second,
     *         <code>false</code> otherwise.
     */
    public static boolean lineSegmentTouchesOrCrossesLine(LineSegment a,
            LineSegment b) {
        return isPointOnLine(a, b.first)
                || isPointOnLine(a, b.second)
                || (isPointRightOfLine(a, b.first) ^ isPointRightOfLine(a,
                        b.second));
    }

    /**
     * Check if line segments intersect
     * @param a first line segment
     * @param b second line segment
     * @return <code>true</code> if lines do intersect,
     *         <code>false</code> otherwise
     */
    public static boolean doLinesIntersect(LineSegment a, LineSegment b) {
        Point[] box1 = a.getBoundingBox();
        Point[] box2 = b.getBoundingBox();
        return doBoundingBoxesIntersect(box1, box2)
                && lineSegmentTouchesOrCrossesLine(a, b)
                && lineSegmentTouchesOrCrossesLine(b, a);
    }
}

Addendum

Some notes for me:

Writing Tests first is worth the effort. I guess it finally saved me some time and it gives me some confidence that my code works.
I should update my system. I'm still using Ubuntu 10.04.4 LTS. Especially, I have Eclipse 3.5.2. This means I could not try EclEmma to test my code coverage ☹
LaTeX is great. I've created all images with LaTeX and it was quite fast after I got the first one. Here is the LaTeX source.

edit: I now have a more modern system. So I was able to use EclEmma, which works fine. And I have 100% branch code coverage for this part of code ☺

How to check if two line segments intersect

Test cases

Bounding boxes

The algorithm

Cross product

Where do two line segments intersect?

TL;DR

Addendum

See also

Published

Category

Tags

Contact