Dieser Artikel beschäftigt sich mit den Vorlesungen des Moduls „Algorithmen II“ am KIT. Er dient als Prüfungsvorbereitung. Ich habe die Vorlesungen bei Prof. Dr. Wagner gehört.
Vorbereitung
Themen:
- Netzwerke und Flüsse
- Wert eines Flusses, s-t-Schnitt
- (Minimale) Schnitte, erhöhende Wege
- Max-Flow Min-Cut Theorem
- Ford-Fulkerson-Algorithmus:
- Erhöhende Wege, Vorwärts- und Rückwärtskanten
- Spezialfall: Algorithmus von Edmonds und Karp
- Kürzeste erhöhende Wege
- Laufzeit: $\mathcal{O}(|V| \cdot |E^2|)$
- Flussproblem als Lineares Programm
- Dualität
- Algorithmus von Goldberg und Tarjan (Residualgraph, Push/Relabel)
- MINCOSTFLOW, erhöhende Kreise
- Cycle Canceling Algorithmus
- Algorithmus von Stoer & Wagner
- Definition: Kreis, einfacher Kreis
- Kreisbasen, Kreisraum
- Matroide
- Zertifikat für MCB
- Las Vegas Algorithmus / Monte Carlo Algorithmus
- Monte Carlo Algorithmus für MinCut
- Fast Random MinCut
- Maximum Satisfiability Problem
- Random MaxCut
- Maximum Satisfiability Problem
- IQP
- Was ist ein einfaches Polygon, was ein konvexes Polygon?
- Sweep Line Algorithmus
- Konvexe Hülle:
- Graham Scan
- Gift Wrapping Algorithmus (Jarvis March) → Code Golf
- Rabin & Karp
- Endlichen Automaten
- Vorberechnungen für viele Suchanfragen:
- Suffixbäume
- Suffixarray
- LCP-Array
- Multiprozessor-Scheduling
- List Scheduling Algorithm
- Bin Packing
- Next Fit Algorithm
- First Fit Algorithm
- APAS
- Restricted Bin Packing
- APAS und FAPAS
- PAS
- FPAS
- Fixed Parameter Tractable
- Kernbildung (Vertex Cover)
- Tiefenbeschrankte Suchbäume
- Job Scheudling
- c-kompetitivität
- Ski-Verleih Beispiel
- Paging (LFD, Kompetitive Paging-Algorithmen, Konservative Paging-Algorithmen, Béládys Anomalie)
- PRAM Modell
- Berechnung von Summen
- Präfxsumme
- List Ranking
- Binaroperationen einer partitionierten Menge
- Zusammenhangskomponenten
- Minimaler Spannbaum
- Einfaches Rechnermodell
- Interner Stack / Externer Stack / Externe Warteschlange
- Multiway Merge Sort
- Tournament-Bäume
Algorithmen und Laufzeiten
| Algorithmus | Laufzeit |
|---|---|
| Algorithmus von Ford und Fulkerson | - |
| Algorithmus von Edmonds und Karp | $\mathcal{O}(|V| \cdot |E|^2)$ |
| Algorithmus von Stoer und Wagner | $\mathcal{O}(|V|^3)$ oder besser, je nach Wahl des aktiven Knotens |
| Algorithmus von Stoer und Wagner | $\mathcal{O}(|V|^2 \log |V| + |V| |E|)$ |
| Algorithmus von Horton | $\mathcal{O}(|E|^3 |V|)$ |
| Algorithmus von de Pina | $\mathcal{O}(|E|^3 + |E| |V|^2 \log |V|)$ |
| Sweep-Line-Algorithmus | $\mathcal{O}(n \cdot \log n)$ |
| Graham-Scan | $\mathcal{O}(n \cdot \log n)$ |
| Gift-Wrapping (Jarvis' March) | $\mathcal{O}(h \cdot n)$ |
| Algorithmus von Rabin und Karp | $\mathcal{O}((n-m) \cdot m)$ |
| String-Matching-Automat | Vorbereitung: $\mathcal{O}(|\Sigma| \cdot m^3)$ Matching: $\mathcal{O}(n)$ |
| Suffix-Bäume | Vorbereitung: $\mathcal{O}(n^2)$ Matching: $\mathcal{O}(m \cdot \log |\Sigma|)$ |
| Suffix-Arrays | Vorbereitung: $\mathcal{O}(n)$ Matching: $\mathcal{O}(m \cdot \log |n|)$ |
Komplexitätsklassen
Die Klasse $\mathcal{PP}$ (probabilistic polynomial) enthält alle Entscheidungsprobleme $\Pi$, für die es einen polynomialen, randomisierten Algorithmus $A$ gibt, so dass für alle Instanzen $I$ von $\Pi$ gilt:
$
\begin{cases}
I \in Y_\Pi & Pr[A(I) \text{ ist "Ja"}] \ge \frac{1}{2} \\
I \notin Y_\Pi & Pr[A(I) \text{ ist "Ja"}] \le \frac{1}{2}
\end{cases}$
Die Klasse $\mathcal{BPP}$ (bounded error PP) enthält alle Entscheidungsprobleme $\Pi$, für die es einen polynomialen, randomisierten Algorithmus $A$ gibt, so dass für alle Instanzen $I$ von $\Pi$ gilt:
$
\begin{cases}
I \in Y_\Pi & Pr[A(I) \text{ ist "Ja"}] \geq \frac{3}{4} \\
I \notin Y_\Pi & Pr[A(I) \text{ ist "Ja"}] \leq \frac{1}{4}
\end{cases}$
Die Klasse $\mathcal{RP}$ (randomisiert polynomial) enthält alle Entscheidungsprobleme $\Pi$, für die es einen polynomialen, randomisierten Algorithmus $A$ gibt, so dass für alle Instanzen $I$ von $\Pi$ gilt:
$
\begin{cases}
I \in Y_\Pi & Pr[A(I) \text{ ist "Ja"}] \geq \frac{1}{2} \\
I \notin Y_\Pi & Pr[A(I) \text{ ist "Ja"}] = 0
\end{cases}$
Es gilt: $\mathcal{RP} \subseteq \mathcal{BPP} \subseteq \mathcal{PP}$
Die Klasse $\mathcal{NC}$ (Nick's Class) ist die Klasse der Probleme, die durch einen parallelen Algorithmus $A$ mit polylogarithmischer Laufzeit und polynomieller Prozessorenzahl gelöst werden können, d.h. $T_A(n) \in \mathcal{O}((\log n)^k_1)$ mit Konstante $k_1$ und $P_A(n) \in \mathcal{O}(n^{k_2})$ mit Konstante $k_2$.
Die Klasse $\mathcal{SC}$ (Steve's Class) ist die Klasse der Probleme, die durch einen sequentiellen Algorithmus mit polylogarithmischem Speicherplatzbedarf und polynomieller Laufzeit gelöst werden können.
Übungsblätter
Übungsblatt 1, 06.02.2013: Lösung
- Amortisierte Laufzeitanalyse: Buchungsmethode
- Was ist ein Netzwerk? Was ist ein Fluss? Was sind die Kapazitätsbedingung und die Flusserhaltung?
Übungsblatt 2, 13.02.2013: Lösung
- Wie bekommt man aus dem maximalen Fluss den minimalen Schnitt mit Push-Relabel?
- Berechnung eines Matchings mit hilfe eines MAX-FLOW-Algorithmus.
- Wie benutze ich den Algorithmus von Stoer und Wagner?
- Funktioniert für negative Kantengewichte nicht, z.B. Graph mit 3 Knoten und 2 negativen Kanten.
Übungsblatt 3, 20.02.2013: Lösung
- Algorithmus von de Pina ausführen (Vorlesung Nr 7)
- Einiges zu Kreisbasen
- Wie bekomme ich mit einem nicht-perfektem Münzwurf eine 50%-Wahrscheinlichkeit? → Antwort
Übungsblatt 4, 20.02.2013: Lösung
- Wie finde ich heraus, ob sich zwei gegebene Strecken schneiden? → Antwort
Übungsblatt 5, 22.02.2013: Lösung
- Wie berechnet man den Suffix-Baum und das Suffix-Array von mississippi? → Vorlesung Nr 13
- Wie funktioniert der Rabin-Karp-Algorithmus zum String-Matching?
- Wie erstellt man einen String-Matching-Automaten?
Übungsblatt 6, 24.02.2013: Lösung
- Welcher Algorithmus für Vertex Cover hat eine Approximationsgüte von 2?
Fakten und interessante Fragen
- Algorithmus ist konservativ $\Rightarrow$ Algorithmus ist k-kompetitiv. (Quelle: Begleitmaterial zur Vorlesung Online-Algorihmen, Uni Dortmund)
- $c(S, V \setminus S) := \sum_{(i,j) \in E,\\i \in S, j \in V \setminus S} c(i,j)$
Was ist der Worst-Case für List Scheduling mit $m$ Maschinen?
Gegeben seien $n \cdot (m-1)$ Jobs à 1 Sekunde und ein Job mit $n$ Sekunden. Die Gesamtlaufzeit beträgt dann $2 \cdot n - 1$ Sekunden, die beste Laufzeit ist jedoch $n$ Sekunden.
Was ist der Worst-Case für Next Fit?
$n$ Elemente mit dem Gewicht $\frac{1}{2}$ und $2n$ Elemente mit dem Gewicht $\frac{1}{2}$ und $2n$ Elemente mit dem Gewicht $\frac{1}{2 \cdot n}$.
Termine und Klausurablauf
Datum: Freitag, den 1. März 2013 von 11:00 bis 13:00 (Quelle)
Ort: Tulla-Hörsaal (Siehe Liste)
Dauer: 2 Stunden
Punkte: 60
Bestehensgrenze: 20
Übungsschein: Gibt es nicht.
Bonuspunkte: Gibt es nicht.
Nicht vergessen:
- Studentenausweis
- Kugelschreiber
Ergebnisse
Der Termin für die Klausureinsicht ist noch nicht bekannt (Stand: 01.03.2013)
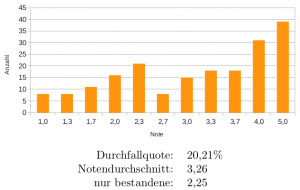
Seit heute (07.03.2013) sind die Ergebnisse da:
- Ergebnisse
- Musterlösung
- Termin der Einsicht ist noch nicht bekannt (Stand: 07.03.2013)
Update vom 09.03.2013: Einsicht ist am Dienstag, den 19. März von 15:00 bis 17:00 Uhr und am Donnerstag, den 4. April von 15:00 bis 17:00 jeweils in Raum 301 im Infobau 50.34