Algorithmen-Klausur

Für die Klausur in Algorithmen I sollte man Folgendes auf jeden Fall wissen:

• Wie sind die Landau-Symbole $\cal O(f(n)), \Theta(f(n)), \Omega(f(n))$ definiert? → Antwort
• Wie lautet das Master-Theorem? → Antwort
• Wie funktioniert der Bellman-Ford-Algorithmus und was macht er? → Antwort
• Wie funktioniert der Dijkstra-Algorithmus und was macht er? → Antwort
• Wie funktioniert der Algorithmus von Kruskal und was macht er? → Antwort
• Wie funktioniert der Algorithmus von Prim und was macht er? → Antwort
• Was ist ein Heap, ein B-Baum, ein Digitaler Baum und was ein Suchbaum? → Antwort
• Sei $A :=$ {Insertionsort, Quicksort, Mergesort, Heapsort, Selectionsort}. Beantworte und begründe für $x \in A$ folgende Fragen:
  • Wie funktioniert x?
  • Ist x stabil?
  • Arbeitet x in-place?
  • Hat x im Worst-Case optimales Laufzeitverhalten?
  • Hat x im Worst-Case optimales Speicherplatzverhalten?
  → Antwort
• Wie funktioniert Radixsort? → Antwort
• Warum ist Radixsort und Countingsort nur schlecht mit den Sortieralgorithmen aus vergleichbar?
• Welches Worst-Case Laufzeitverhalten hat die Breitensuche, welches die Tiefensuche?

Some Random Facts

Das ist ein Graph, bei dem der Algorithmus von Dijkstra fehlschlägt:

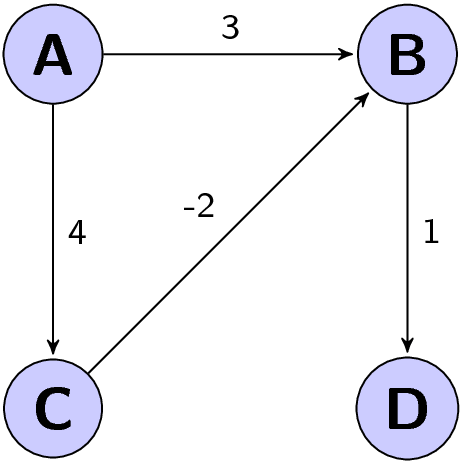
Termine

Datum: Dienstag, der 31.07.2012 um 17:00 Uhr
Ort:

Die Sitze sind alphabetisch nach Ihrem Nachnamen eingeteilt:
A-C Hörsaal am Fasanengarten(50.35)
D-J Gerthsen Hörsaal(30.21)
K-O Audimax(30.95)
P-R Daimler(10.21)
S Benz(10.21)
T-V Tulla(11.40)
W-Z Neue Chemie(30.46)

Dauer: 120 min. (Quelle)
Punkte: 60
Übungsschein: Gibt es nicht. Bonuspunkte gibt es auch nicht.
Sitzplatzverteilung: hier

Nicht vergessen

• Studentenausweis
• Kugelschreiber

Klausurergebnisse

Die Klausurergebnisse hängen im SCC, 3. OG, aus.

Klausureinsicht: 23.08.2012 und 24.08.2012