- Problem A (Osmos):
- Small Set: 4668/7250 users (64%)
- Large Set: 3537/4578 users (77%)
- Problem B (Falling Diamonds):
- Small Set: 952/1882 users (51%)
- Large Set: 525/724 users (73%)
- Problem C (Garbled Email):
- Small Set: 444/896 users (50%)
- Large Set: 255/345 users (74%)
More information are on go-hero.net.
Osmos
#!/usr/bin/env python
# -*- coding: utf-8 -*-
def howBigDoIget(A, motes):
while len(motes) > 0 and A > min(motes):
A += min(motes)
motes.remove(min(motes))
return A
def stepsNeededForNext(A, motes):
m = min(motes)
steps = 0
if m >= 1 and A == 1:
return 10 ** 12
while A <= m:
A += A - 1
steps += 1
return steps
def solve(A, motes):
steps = 0
A = howBigDoIget(A, motes)
while len(motes) > 0 and A <= max(motes):
if stepsNeededForNext(A, motes) >= len(motes):
steps += len(motes)
return steps
else:
A += A - 1
A = howBigDoIget(A, motes)
steps += 1
return steps
if __name__ == "__main__":
testcases = input()
for caseNr in range(1, testcases + 1):
A, N = map(int, raw_input().split(" "))
motes = sorted(map(int, raw_input().split(" ")))
copyed = motes[:]
solution = solve(A, motes)
if solution > N:
solution = N
print("Case #%i: %s" % (caseNr, solution))
Falling Diamonds
Once you've read the task, you should understand some very basic ideas:
- First of all, diamonds only fall at $x=0$ !
- If your target coordinates are $(x,y)$ , you have the same output as for $(-x,y)$ , as everything is symmetric.
- You have to get a basis for your diamonds pyramid. I've colored the basis in yellow in the images below.
- When your target is above the ground, you can let the diamond slide down to calculate the size of the basis.
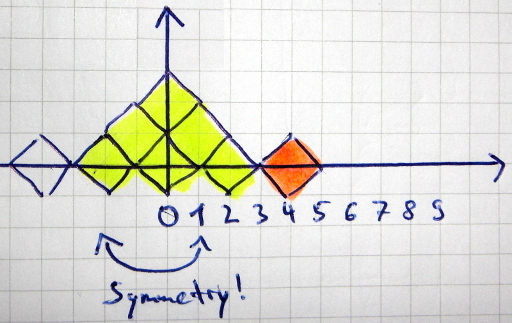
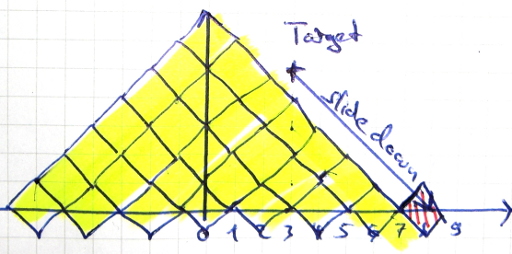
Note that you don't have to calculate a probabilty for the yellow pyramids. You get those with probability of 1.
What I've forgot: You should also catch the case that you can fill up the next bigger pyramid. If this is possible, you can guarantee that you will reach your target $(x,y)$.
The rest is simple math. You have $rest$ diamonds left after you've build the base (yellow). Then you need $y+1$ diamonds slide to the right side. The probability that you have exactly $k$ hits while making $N$ tries with a probability of 50% is $\binom{N}{k} \cdot (\frac{1}{2})^N$. You want at least $k$ hits, so you want $\sum_{i=k}^N \binom{N}{i} \cdot (\frac{1}{2})^N$.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import gmpy
""" Calculate the binomial coefficient """
def binomial(n, k):
return gmpy.comb(n, k)
def solve(N, x, y):
"""
@param N: Number of diamonds
@param x,y: Target coordinate
@return: possiblity, that a diamond will be at coordinate (x,y)
"""
if x == 0:
n = y + 1
if N >= (n * n + n) / 2:
return 1.0
else:
return 0.0
# From this point, x != 0 is True
xTmp = x + y # let target slide down
n = xTmp - 1
baseDiamands = (n ** 2 + n) / 2
# are there enough diamonds left after you've build the basis?
rest = N - baseDiamands
if rest <= 0:
return 0.0
# are there enough diamonds left so that you can guarantee that
# you will fill up the next bigger pyramid at least to the
# target position?
biggerBaseDiamonds = baseDiamands + n + 2 + y
if N >= biggerBaseDiamonds:
return 1.0
# some math:
# bernoulli
prob = 0.0
hitsNeeded = y + 1
for k in range(hitsNeeded, rest + 1):
prob += binomial(rest, k)
return prob / 2 ** rest
if __name__ == "__main__":
testcases = input()
for caseNr in range(1, testcases + 1):
N, x, y = map(int, raw_input().split(" "))
print("Case #%i: %.9Lf" % (caseNr, solve(N, abs(x), y)))