Everybody who has written a noticeable amount of Java code should know the method hashCode(). But most beginners have difficulties to understand the significance of this little method. The following article gives you one small example with some impressions how much hash functions influence execution time.
Connect four
Connect Four [...] is a two-player game in which the players first choose a color and then take turns dropping colored discs from the top into a seven-column, six-row vertically-suspended grid. The pieces fall straight down, occupying the next available space within the column. The object of the game is to connect four of one's own discs of the same color next to each other vertically, horizontally, or diagonally before your opponent.
Source: Wikipedia
It looks like this:

Source: commons.wikimedia.org
The task
Imagine you would like to find a good strategy where to drop your disk. A simple brute-force method is to create a so called game tree. This means you go through each possibility at each situation that could occur in the game for both players.
This approach has generally two problems:
- You have to know how to go through each situation. For connect four it is easy. Both players place their disks in turns and in every turn the current player has at most 7 possibilities. But it is impossible for games like Calvinball or Mao.
- The game tree might be HUGE. In this case, you can have $4,531,985,219,092 \approx 4.5 \cdot 10^{12}$ game situations (source). Even if you would need only one bit for each situation, it would require 566.5 GB!
Anyway, lets say we want to store many unique game situations. Unique means, even if you have hundreds of possible paths to get to a given game situations, you will store this game situation only once.
Implementation
First of all, I would like to mention that you can skip the source code. I've only included it to make it easier to understand what I'm talking about.
Lets say our game situation looks like this:
struct gamesituation {
/** How does the board currently look like? */
char board[BOARD_WIDTH][BOARD_HEIGHT];
/**
* What are the next game situations that I can reach from this
* board?
* The next[i] means that the player dropped the disc at column i
*/
int next[7];
/* I could use a bitfield for this ... but it would make access
* much more inconvenient.
*/
unsigned char isEmpty; // Is this gamesitatution already filled?
unsigned char isFinished; // Is this game finished?
unsigned char stalemate; // Was this game a stalemate?
unsigned char winRed; // Did red win?
unsigned char winBlack; // Did black win?
};
You need a check if one player won:
/*
* Check if player has won by placing a disc on (x,y).
* with direction (xDir, yDir)
* @return 1 iff RED won, -1 iff BLACK won and 0 if nobody won
*/
signed char hasPlayerWon(char board[BOARD_WIDTH][BOARD_HEIGHT],
int x, int y, char xDir, char yDir) {
char color = board[x][y];
int tokensInRow = getTokensInRow(board, color, x, y, xDir, yDir)
+ getTokensInRow(board, color, x, y, -xDir, -yDir) - 1;
if (tokensInRow >= WINNING_NR) {
if (color == RED) {
return 1;
} else if (color == BLACK) {
return -1;
} else {
perror("this color doesn't / shouldn't exist\n");
exit(1);
}
}
return 0;
}
/*
* A new disc has been dropped. Check if this disc means that
* somebody won.
* @return 1 iff RED won, -1 iff BLACK won, otherwise NOT_FINISHED
*/
int isBoardFinished(char board[BOARD_WIDTH][BOARD_HEIGHT],
int x, int y) {
signed char status;
// check left-right
status = hasPlayerWon(board, x, y, 1, 0);
if (status != 0) {
return status;
}
// top-down
status = hasPlayerWon(board, x, y, 0, 1);
if (status != 0) {
return status;
}
// down-left to top-right
status = hasPlayerWon(board, x, y, 1, 1);
if (status != 0) {
return status;
}
// top-left to down-right
status = hasPlayerWon(board, x, y, -1, 1);
if (status != 0) {
return status;
}
return NOT_FINISHED;
}
If you need an explanation for this, you should read this article.
And you need a function that can mirror boards (to get rid of identical, but mirrored situations) and one that can compare boards:
char isSameBoard(char a[BOARD_WIDTH][BOARD_HEIGHT],
char b[BOARD_WIDTH][BOARD_HEIGHT]) {
for (int x = 0; x < BOARD_WIDTH; x++) {
for (int y = 0; y < BOARD_HEIGHT; y++) {
if (a[x][y] != b[x][y]) {
return FALSE;
}
}
}
return TRUE;
}
void mirrorBoard(char board[BOARD_WIDTH][BOARD_HEIGHT],
char newBoard[BOARD_WIDTH][BOARD_HEIGHT]) {
for (int x = 0; x < BOARD_WIDTH; x++) {
for (int y = 0; y < BOARD_HEIGHT; y++) {
newBoard[BOARD_WIDTH - x - 1][y] = board[x][y];
}
}
}
You need a function that makes all possible moves for the players:
/*
* Make all possible turns that the player can make in this
* game situation.
*/
void makeTurns(char board[BOARD_WIDTH][BOARD_HEIGHT],
char currentPlayer, unsigned int lastId, int recursion) {
unsigned int insertID;
int outcome;
for (int column = 0; column < BOARD_WIDTH; column++) {
// add to column
int height = BOARD_HEIGHT - 1;
// the disc falls down
while (height >= 0 && board[column][height] == EMPTY) {
height--;
}
height++;
// this colum is full
if (height == 6) {
continue;
}
// place disc
board[column][height] = currentPlayer;
if (didBoardAlreadyOccur(board)) {
// I've already got to this situation
insertID = getBoardIndex(board);
savePreviousID(insertID, lastId, column);
} else {
char mirrored[BOARD_WIDTH][BOARD_HEIGHT];
mirrorBoard(board, mirrored);
if (didBoardAlreadyOccur(mirrored)) {
// I've already got this situation, but mirrored
// so take care of symmetry at this point
mirroredCounter++;
insertID = getBoardIndex(mirrored);
savePreviousID(insertID, lastId, column);
} else {
registeredSituations++;
if (registeredSituations == MAXIMUM_SITUATIONS) {
giveCurrentInformation();
exit(MAXIMUM_SITUATIONS_REACHED_EXIT_STATUS);
}
if (REGISTERED_MOD > 0 &&
registeredSituations % REGISTERED_MOD == 0) {
giveCurrentInformation();
}
outcome = isBoardFinished(board, column, height);
if (ABS(outcome) <= 1) {
// the game is finished
insertID = getNewIndex(board);
storeToDatabase(insertID, board, TRUE, outcome);
savePreviousID(insertID, lastId, column);
} else {
// Switch players
if (currentPlayer == RED) {
currentPlayer = BLACK;
} else {
currentPlayer = RED;
}
insertID = getNewIndex(board);
setBoard(insertID, board);
savePreviousID(insertID, lastId, column);
char copy[BOARD_WIDTH][BOARD_HEIGHT];
for (int x = 0; x < BOARD_WIDTH; x++) {
for (int y = 0; y < BOARD_HEIGHT; y++) {
copy[x][y] = board[x][y];
}
}
makeTurns(copy, currentPlayer, insertID,
recursion + 1);
}
}
}
}
}
How is this realated to hash functions?
You might have noticed a few functions that I didn't explain by now:
didBoardAlreadyOccur(board): Checks if a given board is stored in database.getBoardIndex(board): This is a function that takes a board and gives a non-negative integer which is characteristic for the given board.savePreviousID(insertID, lastId, column): store insertID as a possible next situation for lastId in databasesetBoard(insertID, board): Insert board into database at position insertID
How would you implement didBoardAlreadyOccur(board)? This function (or insertID) will be the slowest part of the code and will be called VERY often. So it needs to be as fast as possible.
A hash function
Most of the time you can create hash functions by mapping values to integers. In my case, I mapped the board - which is a two-dimensional char array - to one integer by thinking of it as a very long number. I think of a red disc as the digit 1, a black disc as the digit 2 and an empty field as 0:
unsigned int charToInt(char x) {
if (x == RED) {
return 1;
} else if (x == BLACK) {
return 2;
} else {
return 0;
}
}
When you want to get the board number, you can get it like this:
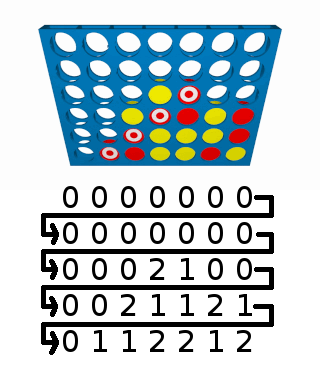
The board number is 00000000000000000210000211210112212
For most game situations, this number will be much too big to store it in an integer. Also, we would like to get an index for our array so that we know where to store this board. The simplest solution to this problem is to calculate NUMBER % ARRAY_SIZE:
unsigned int getFirstIndex(char board[BOARD_WIDTH][BOARD_HEIGHT]) {
unsigned int index = 0;
for (int x = 0; x < BOARD_WIDTH; x++) {
for (int y = 0; y < BOARD_HEIGHT; y++) {
index += charToInt(board[x][y]) *
myPow(3, ((x + y * BOARD_WIDTH) % HASH_MODULO));
}
}
index = index % MAXIMUM_SITUATIONS;
return index;
}
The function getFirstIndex maps an char Array with BOARD_WIDTH * BOARD_HEIGHT = 7 * 6 = 42 elements to an integer interval [0, MAXIMUM_SITUATIONS] = [0, 20000000]. Although I only use three values for the char array, that is $3^{42} = 109418989131512359209 \approx 1.09 \cdot 10^{20}$. There are many game situation numbers that can never occur (e.g. two more red than black dists), but we still map a significantly larger space to [0,20000000]. You can't change that. You can probably find (much) better mappings, but as we know that there are $4.5 \cdot 10^{12}$ game situations, you will always have the problem that your codomain is much smaller than the domain of your hash function. That's a fundamental problem of hash functions.
This means, you will have two board situations that map to the same hash number. This is called a "hash collision". When you use the hash number directly as an index for your board, you will have to deal with hash collisions. Some solutions are:
- Ignoring the problem: That's boring and not always possible (but simple).
- Linear probing
- Quadratic probing
Linear probing
The idea of linear probing is very simple:
Inserting a new item:
- You look at the index $i$ that your hash function gave you.
- If this index is already full, you look at $i+1$
- When you took a look at all slots of your array, you can't insert the new item.
Searching for an already inserted item:
- You look at the index $i$ that your hash function gave you.
- If $i$ is empty, you're ready. The item was not inserted.
- If $i$ is not the item you've searched for, you have to look at $i+1$.
- Keep looking at the next item until you find your searched item, you've looked at all items or you find an empty slot.
Deleting is complicated. You have to look at all items after the deleted one, remove them from your array and insert them again. That's not good.
The problem of linear probing is clustering. When you have some hash values that are close together, you might get hash collisions faster. When you've got your first collisions, you resolve them by inserting the value close to the value where you originally wanted to save it. So you get one big cluster quite fast. When you want to insert an element in the cluster, you first have to search the end of the cluster. That's bad for performance.
An advantage of linear probing compared to quadratic probing is that you might get a better performance due to cache effects.
Quadratic probing
The idea of quadratic probing is the same as for linear probing, but you try to fix the clustering-problem by using a clever way to search for a free spot:
$h_i(x) = \left(h(x) + (-1)^{i+1} \cdot \left\lceil\frac{i}{2}\right\rceil^2\right) \bmod~m$
where $h$ is your hash function and $i$ is your i-th try to find a free spot while you have $m$ spots in total.
This one also suffers from clustering, but it's not as bad as with linear clustering.
Double hashing
This solution could be the best one, but also the hardest one to implement correctly. You could find a free spot by using a second hash function $h'$ like this:
$h_i(x) = (h(x)+h'(x)\cdot i) ~ \bmod ~ m$
BUT you have to make sure that $Pr[h(x)=h(y) \land h'(x)=h'(y)] = \frac{1}{m^2}$
Performance
You can use linear probing, quadratic probing and double hashing in my example and measure how many game situations get stored. The more game situations you can store in the same amount of time, the better:
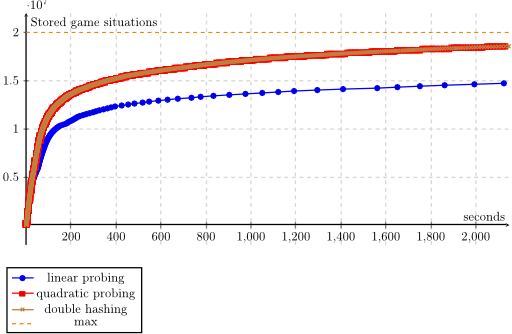
You can see that linear probing performs much worse than quadratic probing and double hashing. When you compare quadratic probing with double hashing, there seems not to be a big difference. But note that my second hash function is almost the same as the first one. You could probably choose a better second hash function and get better results (suggestions are welcome).
Why are hash functions important?
Hash functions help you to map a big amount of data to a small space. They are important, because they are a relevant part of many datastructures. The better they are, the faster will operations on those datastructures work. Better means: Faster to compute or less collisions.
Some datastructures like this are:
- HashMap and HashTable (→ difference)
- HashSet
Final notes
Another resolution for hash collisions is creating a linked list. This means you will not suffer from clustering and you can insert in $\mathcal{O}(1)$. But searching for an element is still in $\mathcal{O}(n)$, where $n$ is the number of elements that were already inserted.
Resources
You can find the code at GitHub.