Komplexitätsklassen werden in der Theoretischen Informatik verwendet um den Ressourcenbedarf von Algorithmen bzw. Problemen einzuordnen. Meist betrachtet man die Laufzeit- und die Speicherplatzkomplexität, aber es wäre prinzipiell auf Vorstellbar, dass man andere Kriterien nutzt. Ich werde in diesem Artikel mal kurz die in der Vorlesung behandelten Klassen vorstellen.
Da es umständlich ist, werde ich im Folgenden nur noch von Problemen reden. Gemeint sind aber meist auch formale Sprachen und Algorithmen.
Die Klasse P
In der Klasse $\cal P$ sind alle Probleme, die mit einer deterministischen Turingmaschine in polynomialzeit lösbar sind. Das sind also alle Probleme, für die es einen Algorithmus gibt, der in $\cal O(n^i), i \in \mathbb{N}_0$ ist.
Wenn es allerdings noch keinen Algorithmus gibt, der ein Problem in polynomialzeit löst, kann das Problem dennoch in $\cal P$ liegen. Dann muss es einen besseren Algorithmus zur Lösung des Problems geben.
Die Klasse NP
In der Klasse $\cal NP$ sind alle Probleme, die mit einer nicht-deterministischen Turingmaschine in polynomialzeit lösbar sind. Das besondere an einer nicht-determinisitschen Turingmaschine ist das Orakelmodul. Es liefert einfach die Lösung. Wie es das macht, wissen wir nicht. Irgendwie geht es halt. Diese Lösung muss in polynomialzeit von einer deterministischen Turingmaschine verifiziert werden.
Was liegt dann nicht in $\cal NP$? Das Orakelmodul hört sich so mächtig an, dass eventuell alle Probleme in $\cal NP$ liegen könnten. Weit gefehlt. Suchprobleme liegen häufig (aber nicht immer) außerhalb von $\cal NP$. Das sind dann Probleme mit einer Fragestellung à la "Gib eine optimale Tour durch eine gegebene Menge an Städten an". Wenn das Orakel-Modul eine solche Tour liefert, muss der deterministische Teil noch schauen, ob es eventuell eine längere Tour gibt.
Die wohl berühmteste Fragestellung der Theoretischen Informatik lautet nun:
P vs. NP: Gibt es Probleme, die in NP liegen, aber nicht in P?
Es ist wohl anschaulich klar, dass gilt: $\cal P \subset NP$. P vs. NP ist die Frage, ob $\cal P = NP$ oder $\cal P \subsetneq NP$. Oder nochmals anders formuliert: $\cal NP \setminus P \stackrel{?}{=} \emptyset$
Die Klasse NPC
Die Klasse der NP-Vollständigen Probleme ist echt in NP, also $\cal NPC \subsetneq NP$. Das besondere an $\cal NPC$ ist, dass jedes Probleminstanz in $\cal NP$ in eine Instanz eines beliebigen Problems in $\cal NPC$ umgewandelt werden kann.
Das es ein solches Problem gibt, hat Cook 1971 mit SAT gezeigt. Cook hat also anschaulich folgendes gemacht:
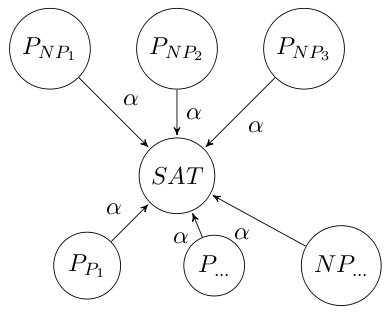
Für alle folgenden Beweise, dass ein Problem in $\cal NPC$ liegt, wurde der Satz von Cook verwendet. Laut diesem Satz (dessen Beweis wahnsinning lang ist) lässt sich jede Probleminstanz von Problemen in $\cal NP$ sich in eine Instanz von SAT umwandeln. Es reicht also zu zeigen, dass sich eine beliebige SAT-Instanz I in eine Instanz I' des neuen Problems in polynomialzeit umwandeln lässt. Diese beiden Instzanzen müssen in folgender Beziehung stehen: Für I existiert eine Lösung $\Leftrightarrow$ für I' existiert eine Lösung:
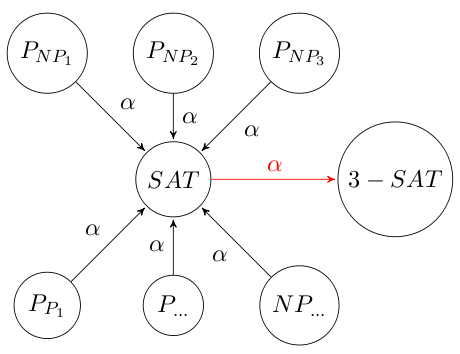
Sobald man von einem Problem sicher weiß, dass es in $\cal NPC$ liegt, kann man natürlich auch etwas anderes als SAT verwenden.
Im Bezug auf P vs. NP ist es vor allem interessant. Wenn ein Problem nicht in P, aber in NP liegt, dann ist sicher jedes Problem in NPC außerhalb von P. Also: $\cal P \neq NP \Rightarrow P \cap NPC = \emptyset$. Warum? Angenommen es existiert ein Problem P für das gilt:
- $P \in \cal NP$
- $P \notin \cal P$
- $P \notin \cal NPC$
Dann gibt es eine polynomielle Transformation von jeder Instanz von P in eine Probleminstanz von einem beliebigem Problem in $\cal NPC$. Damit kann jedes Problem in $\cal NPC$ nicht mehr in $\cal P$ liegen, da sonst auch $P \in \cal P$.
NPI, co-P und co-NP
Formal gilt: $\cal NPI := NP \setminus (P \cup NPC)$. Es sind also alle Probleme, die innerhalb von $\cal NP$ sind, aber außerhalb von $\cal P$ und noch nicht in $\cal NPC$ in $\cal NPI$. Es ist also so eine Art "Zwischenklasse".
Um es etwas anschaulicher zu machen, habe ich mal folgendes Bildchen erstellt:
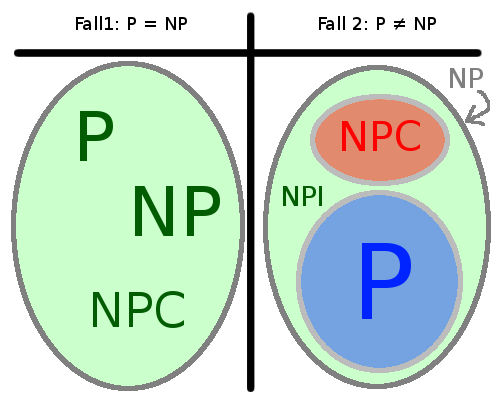
Bemerkenswert ist folgende Aussage: Im Fall $\cal P = NP$ ist auch ${\cal P} \setminus {\emptyset, \Sigma^*} = {\cal NPC}$ (siehe Nachklausur von 2007 / 2008, Frage 5). Warum stimmt das? Damit ein Problem $\in \cal NPC$ ist, muss es nur eine polynomielle Transformation von jedem Problem in NP auf das eine Problem geben. Das ist offensichtlich der Fall, wenn man alle Probleme in NP in polynomieller Zeit lösen kann. In diesem Fall kann man das Entscheidungsproblem lösen und eine Ja-Instanz auf eine beliebige andere Ja-Instanz abbilden und analog Nein-Instanzen auf Nein-Instanzen abbilden. Da $\emptyset$ keine Ja-Instanz hat und $\Sigma$ keine Nein-Instanz hat, muss man diese herausnehmen.
Formal gilt: $\text{co-}{\cal P} := {L \in \Sigma^ | L^C \in {\cal P}}$ und analog $\text{co-}{\cal NP} := {L \in \Sigma^ | L^C \in {\cal NP}}$.
Folgende Aussage finde ich dazu sehr interessant: $L \in {\cal NPC} \land L \in \text{co-}{\cal NP} \Rightarrow {\cal NP} = \text{co-}{\cal NP}$
D-TAPE und N-TAPE
Im Skript wurde das seltsam geschrieben ($\cal DTAPE$). Ich habe so nicht mehr erkannt, dass es TAPE heißen soll. In der Klausur sollte man sich davon nicht irritieren lassen.
Formal: $D-TAPE(s(n)) := {L | \text{Es existiert eine determinitistische TM, die L mit Platzbedarf s(n) akzeptiert.}}$ $N-TAPE(s(n)) := {L | \text{Es existiert eine nicht-determinitistische TM, die L mit Platzbedarf s(n) akzeptiert.}}$
Quellen und Material
- Theoretische Grundlagen der Informatik: Skript von Prof. Dr. Dorothea Wagner
- Die Bilder stehen hier zur Verfügung: Material zu den Komplexitätsklassen