Project Euler: Problem 142

Project Euler is a series of challenging mathematical/computer programming problems that will require more than just mathematical insights to solve. Although mathematics will help you arrive at elegant and efficient methods, the use of a computer and programming skills will be required to solve most problems.

The motivation for starting Project Euler, and its continuation, is to provide a platform for the inquiring mind to delve into unfamiliar areas and learn new concepts in a fun and recreational context.

Today, I would like to discuss problem 142. I've seen a post from Santiago Alessandri, so I liked to do the task by myself.

The task is:

Find the smallest x + y + z with integers $x > y > z > 0$ such that x + y, x - y, x + z, x - z, y + z, y - z are all perfect squares.

I don't want to post the solution (if you want to cheat, I guess you could easily Google it), but some thoughts that might help you to get in the right direction.

First thought: Brute-force

Brute-force is the easiest way that could give you the solution. So I wrote this piece of code:

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import sys
from math import sqrt


def is_square(integer):
    root = sqrt(integer)
    if int(root + 0.5) ** 2 == integer:
        return True
    else:
        return False


for x in range(3, 1000):
    print(x)
    for y in range(2, x):
        for z in range(1, y):
            if x > y and y > z:
                if (
                    is_square(x + y)
                    and is_square(x - y)
                    and is_square(x + z)
                    and is_square(x - z)
                    and is_square(y + z)
                    and is_square(y - z)
                ):
                    print("%i - %i - %i" % (x, y, z))
                    sys.exit()

This is quite fast until you reach about 500. So this is not a good way to solve it.

Apply some math

You can formalize the task like this: Find the smallest \(x, y, z \in \mathbb{N}\), so that:

1. $x > y > z > 0$
2. $a = x + y$
3. $b = x - y$
4. $c = x + z$
5. $d = x - z$
6. $e = y + z$
7. $f = y - z$

With \(a, b, c, d, e, f \in Squares\).

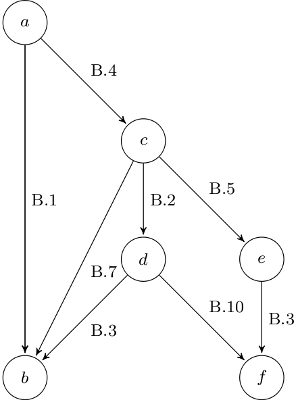
Now you can make the following conclusions:

1. $\overset{A.1, A.2, A.3}{\implies} a > b$
2. $\overset{A.1, A.4, A.5}{\implies} c > d$
3. $\overset{A.1, A.6, A.7}{\implies} e > f$

1. \(a > c\): \(y > z\) \(\Leftrightarrow x + y > x + z\) \(\Leftrightarrow a > c\)

2. \(c > e\): \(x > y\) \(\Leftrightarrow x + z > y + z\) \(c > e\)

3. a is the biggest element (see B.1, B.4, B.6)

4. \(b < c\): \(-y < z\) \(\Leftrightarrow x - y < x + z\) \(b < c\)

5. c is the second biggest element (see B.7, B.2, B.5, B.8)

6. \(b < d\): \( y > z\) \(\Leftrightarrow -y < -z\) \(\Leftrightarrow x - y < x - z\) \(b < d\)

7. \(d > f\): \( x > y\) \(\Leftrightarrow x - z > y - z\) \(d > f\)

8. I can't tell anything about the relationship between:

• d and e
• b and f
• b and e

Lets conclude:

You also know:

\(x = \frac{a - b}{2} \implies \text{ (a - b) has to be even} \implies \text{a and b have the same parity.}\) The same argumentation can be used for (c, d) and (e, f).

\(x > y > z > 0 \land a = x + y \implies a \geq 5\).

With this in mind you don't have to loop over three variables but only over two. This is much faster. As z is over 1000 you need it. My new script took about 1.5 minutes.

Material

Some material like the LaTeX-file can be found in the Project Euler 142 Archive.