It's astonishing how difficult it is to find a good explanation how to reflect a point over a line that does not use higher math methods. So here is my explanation:
You have a point $P = (x,y)$ and a line $g(x) = m \cdot x + t$ and you want to get the point $P' = (x', y')$ that got mirrored over $g$.
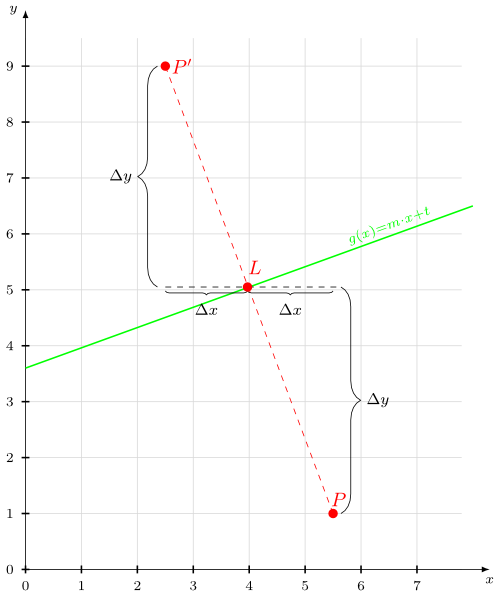
As you can see, you can construct this quite easily on paper:
- Construct the perpendicular through $P$ to $g$. It starts in $L$ and ends in $P$.
- Double the length of the perpendicular in the direction of $L$.
- The endpoint is $P'$.
How can you do that without drawing it?
First you have to get the perpendicular $s(x) = m_s \cdot x + t$ (the dashed red line).
You have to know this: $m_s = - \frac{1}{m}$ And then you know that $P$ is on $s$. So you simply put in the values $x,y$ of P and solve to $t$: $t = y - m_s \cdot x$
Now you have $s$. As $s$ and $g$ have exactly point in common, the following equation gives exactly one result:
$s(x) = g(x)$
You have to solve for $x$. Then you only need to put $x$ into $s(x)$ or $g(x)$ and you're done. You've calculated $L = (x,y)$.
Now you know $\Delta x = |x_L - x_P|$ and $\Delta y = |y_L - y_P|$ and you can calculate $P'$