Siamese Networks are feature extractors trained to learn an embedding in $\mathbb{R}^n$ where not the absolute output is important, but the relative one.
The original paper1 was about signature verification. You have one original signature and one that might be the same or might be a different one. Instead of having one output that directly says "same" or "different", they decided to have one network that maps the input to $\mathbb{R}^{4 \times 19}$ and then use euclidean distance with some threshold2.
Today, the nicest usage I know is DeepFace3. It is a neural network which maps faces to $\mathbb{R}^{128}$ by combining a lot of clever ideas.
Key Idea
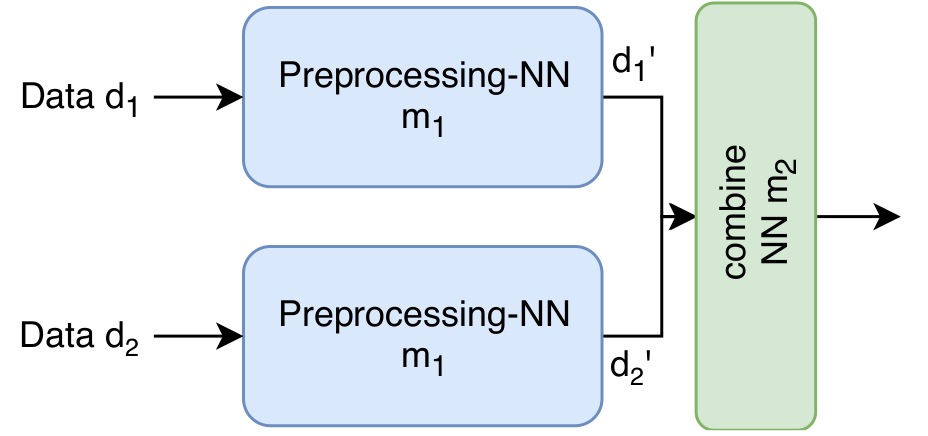
You have one network $m_1$ which is embedded into another network which combines two inputs of $m_1$. So for training a triplet $(d_1, d_2, t)$ is used, where $d_1$ and $d_2$ are both processed individually by $m_1$. The two outputs $d_{1}'$ and $d_{2}'$ are then combined by another network $m_2$. $m_2$ can simply be a merging layer. The loss is then calculated based on the output of $m_2$.
Applications
- Signature Verification: Given two signatures, do they belong to the same person?
- Face Verification: Given two faces, are they the same person?
- Koch, G., Zemel, R., & Salakhutdinov, R. (2015, July). Siamese neural networks for one-shot image recognition. In ICML deep learning workshop (Vol. 2).
- Leal-Taixé, L., Canton-Ferrer, C., & Schindler, K. (2016). Learning by tracking: Siamese CNN for robust target association. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (pp. 33-40).
Application: Landmark Distances
Think of autonomous cars. They might know some landmarks and be able to identify them. Then they can measure the distance to those landmarks. And maybe some landmarks are added later. I wondered how well a neural network does in finding coordinates for landmarks, given distances to existing landmarks.
While this problem is better solved with another approach, I was just curious how well a simple neural network would do. The answer was ... underwhelming. I guess I made an error, but at the moment I can't find it:
#!/usr/bin/env python
"""
Train a neural network on distances and see how well it figures out coordinates.
Roughly siamese networks.
The "reference points" are landmarks
"""
# core modules
from itertools import combinations
from functools import partial
# 3rd party modules
import keras.backend as K
from keras.layers import Dense
from keras.layers import Input, Concatenate
from keras.models import Model
from sklearn.metrics.pairwise import euclidean_distances
import numpy as np
from scipy.spatial.distance import euclidean
from sklearn.model_selection import train_test_split
np.random.seed(0)
def main():
import doctest
doctest.testmod()
# Configure Problem
n_reference_points = 11
n_points = n_reference_points + 30
n_dim = 10
# Define Network for mapping distances to landmarks to point coordinates
nn = create_network(n_reference_points, n_dim)
# Make the network trainable
dists1_in = Input(shape=(n_reference_points,))
dists2_in = Input(shape=(n_reference_points,))
point1_out = nn(dists1_in)
point2_out = nn(dists2_in)
merged_vector = Concatenate(axis=-1)([point1_out, point2_out])
model = Model(inputs=[dists1_in, dists2_in], outputs=merged_vector)
model.compile(loss=partial(dual_loss, n_dim=n_dim), optimizer="adam")
# Generate Data
points = generate_data(n_points=n_points, n_dim=n_dim)
print(points[:n_reference_points])
distances = get_distances(points, n_reference_points)
train_points, test_points, train_distances, test_distances = train_test_split(
points, distances
)
distances_p1s, distances_p2s, pair_distances = get_train_data(
train_points, train_distances
)
model.fit(
[distances_p1s, distances_p2s], pair_distances, batch_size=128, epochs=100
)
predicted_points = nn.predict(test_distances)
error = measure_error(test_points, predicted_points)
print("Error: {:0.3f}".format(error))
error = measure_error(test_points, generate_random(predicted_points.shape))
print("Error (random): {:0.3f}".format(error))
def generate_data(n_points, n_dim):
"""
Generate n_points of dimension n_dim.
Examples
--------
>>> generate_data(1, 2).tolist()
[[0.5488135039273248, 0.7151893663724195]]
"""
points = np.random.random((n_points, n_dim))
return points
def generate_random(shape):
"""Generate a random point coordinate prediction."""
return np.random.random(shape)
def get_distances(points, n_reference_points):
"""
Get the distance of points to the n reference points.
This includes the pair-wise distance between the reference points.
"""
ref_points = points[:n_reference_points]
distances = []
for point in points:
distances.append([])
for ref_point in ref_points:
distances[-1].append(euclidean(point, ref_point))
return np.array(distances)
def create_network(n_reference_points, n_dim):
input_ = Input(shape=(n_reference_points,))
x = input_
x = Dense(200, activation="relu")(x)
x = Dense(200, activation="relu")(x)
x = Dense(n_dim, activation="sigmoid")(x)
model = Model(inputs=input_, outputs=x)
return model
def dual_loss(y_true, y_pred, n_dim=2):
"""
Define the loss function based on two points.
Parameters
----------
y_true : ndarray
The real distance
y_pred : ndarray
The first n_dim elements are the first points coordinates,
the seoncd n_dim elements are the second points coordinates
"""
point1 = y_pred[:, 0:n_dim]
point2 = y_pred[:, n_dim:]
# distance between the points
embedding_dist = K.sum(K.square(point1 - point2), axis=1)
# compute loss
loss = K.abs(embedding_dist - y_true)
return loss
def get_train_data(points, distances):
"""
Create training data.
Parameters
----------
points : List
Returns
-------
(distances_p1, distances_p2, pair_distances) : tuple
distances_p1 and distances_p2 have the same structure (point 1 and
point 2) The contens of those two lists are the distances to the
reference points
pair_distances : The i-th entry contains the distance between
distance_pairs[i][0] and distance_pairs[i][1]
"""
distances_p1 = []
distances_p2 = []
pair_distances = []
for pi1, pi2 in combinations(list(range(len(points))), 2):
p1_dist = distances[pi1]
p2_dist = distances[pi2]
distances_p1.append(p1_dist)
distances_p2.append(p2_dist)
pair_distances.append(euclidean(points[pi1], points[pi2]))
return np.array(distances_p1), np.array(distances_p2), np.array(pair_distances)
def measure_error(real_points, predicted_points):
"""
Measure an error between the real points and the predicted points.
This does not punish the points being shifted / rotated.
"""
real_distances = np.tril(euclidean_distances(real_points), 0).reshape(-1)
pred_point_distances = np.tril(euclidean_distances(predicted_points)).reshape(-1)
diff = sum(((real_distances - pred_point_distances) ** 2) ** 0.5)
return diff / len(real_points)
if __name__ == "__main__":
main()
Footnotes
-
Bromley, Jane, et al. "Signature verification using a" siamese" time delay neural network." Advances in neural information processing systems. 1994. ↩
-
I'm actually not sure which metric they used to calculate the distance between to signature feature matrices. Please ping me if you know more. ↩
-
Taigman, Yaniv, et al. "Deepface: Closing the gap to human-level performance in face verification." Proceedings of the IEEE conference on computer vision and pattern recognition. 2014. (summary) ↩