
|
Warum ist Q abzählbar? |
Recent Posts
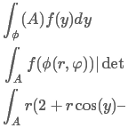
|
Wie wendet man den Transformationssatz an? |
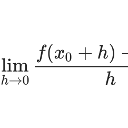
|
Wie zeige ich Differenzierbarkeit? |

|
Integration durch Substitution |
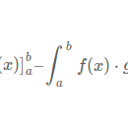
|
Partielle Integration |
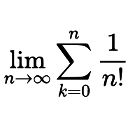
|
Konvergenz von Reihen |
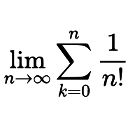
|
Konvergenz von Folgen |