Recent Posts

Solving linear equations with Gaussian elimination Please note that you should use LU-decomposition to solve linear equations. The following code produces valid solutions, but when your vector $b$ changes you have to do all the work again. LU-decomposition is faster in those cases and not slower in case you don't have to solve equations with the … Read More »

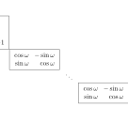
Jordansche Normalform: 4x4 Matrizen Hier sind $4 \times 4$ Beispiele zum Hauptartikel Wie berechnet man die Jordan’sche Normalform?. Beispiel 1 Gegeben sei die Matrix $A \in \mathbb{R}^{4 \times 4}$: $$A := \begin{pmatrix} 1 & 2 & 47 & 11\ 3 & 2 & 8 & 15\ 0 & 0 & 3 & 1\ 0 & 0 & 8 & 1 \end{pmatrix}$$ Jordannormalform … Read More »

Berechnung der euklidischen Normalform Die euklidische Normalform einer linearen Isometrie, manchmal auch lineare Normalform gennant, hat folgende Gestalt: Euklidische Normalform Bei einer $n \times n$-Matrix gilt also folgende Gleichung: $n = p + q + 2r$ Bestimmung der Normalform Sei $\Phi$ eine lineare Isometrie eines euklidischen Vektorraumes. Dann habe $\Phi$ die Abbildungsmatrix $A$. Sei $B := A … Read More »

Jordansche Normalform: 2x2 Matrizen Hier sind $2 \times 2$ Beispiele zum Hauptartikel Wie berechnet man die Jordan’sche Normalform?. Beispiel 1 Gegeben sei die Matrix $A \in \mathbb{R}^{2 \times 2}$: $$A := \begin{pmatrix} 11 & -4\\ 25 & -9 \end{pmatrix}$$ . Jordannormalform bestimmen 1. Charakteristisches Polynom berechnen: $p_A(\lambda) = (\lambda - 1)^2$. Daraus folgt … Read More »

Wie berechnet man die Jordan'sche Normalform? Dieser Artikel beschreibt, wie die Jordansche Normalform einer Matrix sowie die dazugehörige Basiswechselmatrix gefunden werden kann. Dabei wird hier eine Jordansche Normalform erzeugt, bei der die 1er auf der oberen Nebendiagonale sind und die größten Jordankästchen zuerst kommen. Ich werde hier nicht erklären, warum es so funktioniert. Hier sind zwei … Read More »

Wie bestimme ich den Kern einer linearen Abbildung? Definition Der Kern einer linearen Abbildung ist eine Menge von Vektoren. In diesem Artikel erkläre ich kurz und bündig, wie man den Kern einer linearen Abbildung bestimmt. Sei $\Phi: V \rightarrow W$ eine lineare Abbildung. Der Kern von $\Phi$ ist die Menge aller Vektoren von V, die durch $\Phi$ auf … Read More »

Endliche Gruppen Endliche Gruppen haben ein paar interessante Eigenschaften. Unter anderem gibt es nur zwei Gruppen mit vier Elementen. alle anderen Gruppen sind isomorph zu diesen Gruppen. Das zeige ich im folgendem. Gruppen mit vier Elementen Es gibt genau zwei Gruppen mit vier Elementen. Das sind: $G_1 = (\mathbb{Z}/4\mathbb{Z … Read More »

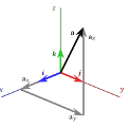
Permutationen und Transpositionen Permutation Definition Es sei M eine endliche Menge. Eine bijektive Selbstabbildung von M heißt Permutation. Die Menge $S_M$ der Permutationen von M ist eine Gruppe bezüglich der Verkettung $\circ$ von Abbildungen und heißt symmetrische Gruppe von M. Quelle: Skript von Herrn Prof. Dr. Leuzinger, KIT Allgemeines Es ist nun egal … Read More »

When is matrix multiplication commutative? Matrix multiplication in general is not commutative. Here is an example: $A, B \in R^{2 \times 2}$ $$A := \begin{pmatrix} 1 & 2 \ 3 & 4 \end{pmatrix}$$ $$B := \begin{pmatrix} 5 & 6 \ 7 & 8 \end{pmatrix}$$ $$A \cdot B = \begin{pmatrix} 19 & 22 \ 43 & 50 \end{pmatrix} \neq \begin{pmatrix … Read More »

Wie berechnet man die Cholesky-Zerlegung? Sei $A \in \mathbb{R}^{n \times n}$ eine symmetrische, positiv definite Matrix. Dann existiert eine Zerlegung $A = S \cdot D \cdot S^T$, wobei $S$ eine unipotente Dreiecksmatrix ist und D eine positiv definite Diagonalmatrix. Berechnung der Cholesky-Zerlegung Hier ein paar Ausschnitte, aus der englischen Wikipedia: Einfach von links … Read More »