Triangle area

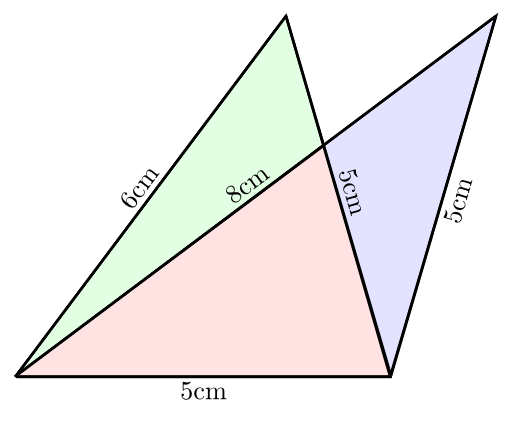
I've just seen the following image on spikedmath.com:

The second answers seem to be obviously the correct ones, right? Wrong.

According to Heron's formula you can calculate a triangles area like this:

Let \(a, b, c\) be the side lengths of the triangle. \(s := \frac{a+b+c}{2}\) \(T = \sqrt{s \cdot (s-a) \cdot (s-b) \cdot (s-c)}\)

So the area of the first triangle is \(s_1 := \frac{16}{2} = 8\) \(T_1 := \sqrt{8 \cdot (8-5) \cdot (8-5) \cdot (8-6)} = \sqrt{8 \cdot 3 \cdot 3 \cdot 2} = 3 \cdot 4 = 12\)

The area of the second one is \(s_1 := \frac{18}{2} = 9\) \(T_1 := \sqrt{9 \cdot (9-5) \cdot (9-5) \cdot (9-8)} = \sqrt{9 \cdot 4 \cdot 4 \cdot 1} = 3 \cdot 4 = 12\)

Both triangles have the same area!

When you draw it, it looks like this: