Übersicht über Datenstrukturen

Diese Übersicht beinhaltet grundlegende Datenstrukturen. Es gibt weitaus mehr Datenstrukturen (z.B. Bloomfilter), als ich hier erwähne. Diese Datenstrukturen wurden in der Vorlesung Algorithmen I bei Frau Zitterbart am KIT erklärt.

Array

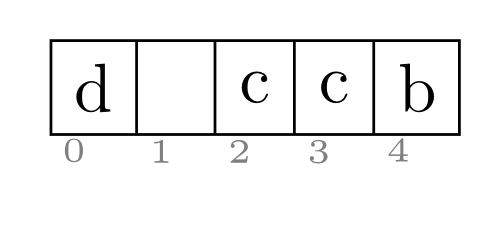
Ein Array, auch Feld genannt, ist eine Datenstruktur. Charakteristika:

Ein Array hat eine feste, nicht veränderbare Größe.
Der Zugriff auf jedes beliebige Element erfolgt in konstanter Zeit - ist also insbesondere unabhängig von der Größe!

Dynamische Arrays

Dynamische Arrays sind wie normale Arrays, nur dass sie wachsen können. Sobald ein Element eingefügt werden soll, dass nicht mehr ins Array passen würde, allokiert man ein doppelt so großes Array und kopiert die Elemente um.

In Java ist es ein Vector bzw. eine ArrayList, in C++ Vektoren.

Hashtabelle

In der Informatik bezeichnet man eine spezielle Indexstruktur als Hashtabelle (englisch hash table oder hash map) bzw. Streuwerttabelle. Als Indexstruktur werden Hashtabellen verwendet um Datenelemente in einer großen Datenmenge aufzufinden. Zu Hashtabellen alternative Index-Datenstrukturen sind beispielsweise Baumstrukturen (wie etwa ein B+-Baum) und die Skip-List. Hashtabellen zeichnen sich durch einen üblicherweise konstanten Zeitaufwand bei Einfüge- bzw. Entfernen-Operationen aus. Beim Einsatz einer Hashtabelle zur Suche in Datenmengen spricht man auch von einem Hashverfahren oder Streuspeicherverfahren.

Quelle: Hashtabelle

Hashtabellen werden hier benutzt:

Python 3.2.3: Modules/_pickle.c
Java OpenJDK 7: java.util.HashTable und sehr viele mehr benutzen es (Properties.java, Dictionary.java, Enum.java, ...)

Sie garantieren eine amortisierte Laufzeit von ${\cal O}(1)$ für Suchen, Löschen und Einfügen.

Folgende Begriffe sollte man kennen:

Divisions-Rest-Methode: $h(k) = k \mod m$
Multiplikationsmethode: $h(k) = \lfloor A \cdot k \mod 1 \rfloor$, mit z.B. $A \approx \frac{\sqrt{5}-1}{2}$
offenes Hashing
Doppeltes Hashing: $h(k, i) = (h_1(k) + i \cdot h_2(k)) \mod m$
Lineares und quadratische Sondieren
Belegungsfaktor: $\alpha = \frac{\text{Anzahl gespeicherter Elemente}}{\text{Anzahl der Slots}}$
Primäre und sekundäre Clusterbildung

Stack

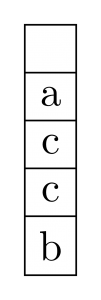
Stacks, auch "Stapelspeicher" oder "Kellerspeicher" genannt, sind eine elementare Datenstruktur. Es sollte sie in jeder Sprache geben. In Java ist es in java.util.Stack, in Python sind es Listen und natürlich gibt es auch in C++ Stacks.

Wie man am Bild sehr schön sehen kann, definiert ein Stack keine Ordnung über die Elemente. Wenn ein neues Element kommt, wird es auf den Stack gelegt. Man kann auch nur das oberste Element - in diesem Fall a - vom Stack nehmen. Deshalb werden Stacks auch als LIFO-Speicher (Last In First Out) bezeichnet.

Stacks werden mit dynamischen Arrays realisiert. Dazu mal ein kleines Beispiel:

import java.util.Stack;

public class test {
    public static void main(String[] args) {
        Stack<Integer> s = new Stack<Integer>();

        s.add(12);
        s.push(13);

        for (int i = 0; i < 100; i++) {
            s.push(i);
            System.out.printf("size: %d \t capacity: %d\n",
                    s.size(), s.capacity());
        }

        while (s.size() > 0) {
            System.out.printf(
                    "Element: %d \t size: %d \t capacity: %d\n",
                    s.pop(),s.size(), s.capacity());
        }
    }
}

Ausgabe:

size: 3      capacity: 10
size: 4      capacity: 10
size: 5      capacity: 10
size: 6      capacity: 10
size: 7      capacity: 10
size: 8      capacity: 10
size: 9      capacity: 10
size: 10     capacity: 10
size: 11     capacity: 20
size: 12     capacity: 20
size: 13     capacity: 20
size: 14     capacity: 20
size: 15     capacity: 20
size: 16     capacity: 20
size: 17     capacity: 20
size: 18     capacity: 20
size: 19     capacity: 20
size: 20     capacity: 20
size: 21     capacity: 40
size: 22     capacity: 40
size: 23     capacity: 40
size: 24     capacity: 40
size: 25     capacity: 40
size: 26     capacity: 40
size: 27     capacity: 40
size: 28     capacity: 40
size: 29     capacity: 40
size: 30     capacity: 40
size: 31     capacity: 40
size: 32     capacity: 40
size: 33     capacity: 40
size: 34     capacity: 40
size: 35     capacity: 40
size: 36     capacity: 40
size: 37     capacity: 40
size: 38     capacity: 40
size: 39     capacity: 40
size: 40     capacity: 40
size: 41     capacity: 80
size: 42     capacity: 80
size: 43     capacity: 80
size: 44     capacity: 80
size: 45     capacity: 80
size: 46     capacity: 80
size: 47     capacity: 80
size: 48     capacity: 80
size: 49     capacity: 80
size: 50     capacity: 80
size: 51     capacity: 80
size: 52     capacity: 80
size: 53     capacity: 80
size: 54     capacity: 80
size: 55     capacity: 80
size: 56     capacity: 80
size: 57     capacity: 80
size: 58     capacity: 80
size: 59     capacity: 80
size: 60     capacity: 80
size: 61     capacity: 80
size: 62     capacity: 80
size: 63     capacity: 80
size: 64     capacity: 80
size: 65     capacity: 80
size: 66     capacity: 80
size: 67     capacity: 80
size: 68     capacity: 80
size: 69     capacity: 80
size: 70     capacity: 80
size: 71     capacity: 80
size: 72     capacity: 80
size: 73     capacity: 80
size: 74     capacity: 80
size: 75     capacity: 80
size: 76     capacity: 80
size: 77     capacity: 80
size: 78     capacity: 80
size: 79     capacity: 80
size: 80     capacity: 80
size: 81     capacity: 160
size: 82     capacity: 160
size: 83     capacity: 160
size: 84     capacity: 160
size: 85     capacity: 160
size: 86     capacity: 160
size: 87     capacity: 160
size: 88     capacity: 160
size: 89     capacity: 160
size: 90     capacity: 160
size: 91     capacity: 160
size: 92     capacity: 160
size: 93     capacity: 160
size: 94     capacity: 160
size: 95     capacity: 160
size: 96     capacity: 160
size: 97     capacity: 160
size: 98     capacity: 160
size: 99     capacity: 160
size: 100    capacity: 160
size: 101    capacity: 160
size: 102    capacity: 160
Element: 99      size: 101   capacity: 160
Element: 98      size: 100   capacity: 160
Element: 97      size: 99    capacity: 160
Element: 96      size: 98    capacity: 160
Element: 95      size: 97    capacity: 160
Element: 94      size: 96    capacity: 160
Element: 93      size: 95    capacity: 160
Element: 92      size: 94    capacity: 160
Element: 91      size: 93    capacity: 160
Element: 90      size: 92    capacity: 160
Element: 89      size: 91    capacity: 160
Element: 88      size: 90    capacity: 160
Element: 87      size: 89    capacity: 160
Element: 86      size: 88    capacity: 160
Element: 85      size: 87    capacity: 160
Element: 84      size: 86    capacity: 160
Element: 83      size: 85    capacity: 160
Element: 82      size: 84    capacity: 160
Element: 81      size: 83    capacity: 160
Element: 80      size: 82    capacity: 160
Element: 79      size: 81    capacity: 160
Element: 78      size: 80    capacity: 160
Element: 77      size: 79    capacity: 160
Element: 76      size: 78    capacity: 160
Element: 75      size: 77    capacity: 160
Element: 74      size: 76    capacity: 160
Element: 73      size: 75    capacity: 160
Element: 72      size: 74    capacity: 160
Element: 71      size: 73    capacity: 160
Element: 70      size: 72    capacity: 160
Element: 69      size: 71    capacity: 160
Element: 68      size: 70    capacity: 160
Element: 67      size: 69    capacity: 160
Element: 66      size: 68    capacity: 160
Element: 65      size: 67    capacity: 160
Element: 64      size: 66    capacity: 160
Element: 63      size: 65    capacity: 160
Element: 62      size: 64    capacity: 160
Element: 61      size: 63    capacity: 160
Element: 60      size: 62    capacity: 160
Element: 59      size: 61    capacity: 160
Element: 58      size: 60    capacity: 160
Element: 57      size: 59    capacity: 160
Element: 56      size: 58    capacity: 160
Element: 55      size: 57    capacity: 160
Element: 54      size: 56    capacity: 160
Element: 53      size: 55    capacity: 160
Element: 52      size: 54    capacity: 160
Element: 51      size: 53    capacity: 160
Element: 50      size: 52    capacity: 160
Element: 49      size: 51    capacity: 160
Element: 48      size: 50    capacity: 160
Element: 47      size: 49    capacity: 160
Element: 46      size: 48    capacity: 160
Element: 45      size: 47    capacity: 160
Element: 44      size: 46    capacity: 160
Element: 43      size: 45    capacity: 160
Element: 42      size: 44    capacity: 160
Element: 41      size: 43    capacity: 160
Element: 40      size: 42    capacity: 160
Element: 39      size: 41    capacity: 160
Element: 38      size: 40    capacity: 160
Element: 37      size: 39    capacity: 160
Element: 36      size: 38    capacity: 160
Element: 35      size: 37    capacity: 160
Element: 34      size: 36    capacity: 160
Element: 33      size: 35    capacity: 160
Element: 32      size: 34    capacity: 160
Element: 31      size: 33    capacity: 160
Element: 30      size: 32    capacity: 160
Element: 29      size: 31    capacity: 160
Element: 28      size: 30    capacity: 160
Element: 27      size: 29    capacity: 160
Element: 26      size: 28    capacity: 160
Element: 25      size: 27    capacity: 160
Element: 24      size: 26    capacity: 160
Element: 23      size: 25    capacity: 160
Element: 22      size: 24    capacity: 160
Element: 21      size: 23    capacity: 160
Element: 20      size: 22    capacity: 160
Element: 19      size: 21    capacity: 160
Element: 18      size: 20    capacity: 160
Element: 17      size: 19    capacity: 160
Element: 16      size: 18    capacity: 160
Element: 15      size: 17    capacity: 160
Element: 14      size: 16    capacity: 160
Element: 13      size: 15    capacity: 160
Element: 12      size: 14    capacity: 160
Element: 11      size: 13    capacity: 160
Element: 10      size: 12    capacity: 160
Element: 9   size: 11    capacity: 160
Element: 8   size: 10    capacity: 160
Element: 7   size: 9     capacity: 160
Element: 6   size: 8     capacity: 160
Element: 5   size: 7     capacity: 160
Element: 4   size: 6     capacity: 160
Element: 3   size: 5     capacity: 160
Element: 2   size: 4     capacity: 160
Element: 1   size: 3     capacity: 160
Element: 0   size: 2     capacity: 160
Element: 13      size: 1     capacity: 160
Element: 12      size: 0     capacity: 160

Wenn man das ausführt, sieht man es recht schnell. Alternativ schaut man in die Dokumentation und liest:

The Stack class represents a last-in-first-out (LIFO) stack of objects. It extends class Vector with five operations that allow a vector to be treated as a stack.

Operation	Worst-Case-Laufzeit	Anmerkungen
Push	${\cal O}(1)$	Ein Element auf den Stack legen
Pop	${\cal O}(1)$	Das oberste Element von der Liste nehmen

Ein Stack lässt sich als doppelt verkettete, zyklische Liste implementieren.

Warteschlangen

Warteschlangen, auch Queues genannt, sind Stacks sehr ähnlich. Beide unterstützen prinzipiell nur zwei Operationen. Bei Stacks nanne es sich PUSH und POP, bei Warteschlangen heißt es ENQUEUE und DEQUEUE. Im Unterschied zum Stack wird bei der Warteschlange das Element nicht von oben wieder weggenommen, sondern von hinten. Das Bild einer Warteschlange ist hier sehr passend.

Operation	Worst-Case-Laufzeit	Anmerkungen
Enqueue	${\cal O}(1)$	Ein Element auf den Stack legen
Dequeue	${\cal O}(1)$	Das oberste Element von der Liste nehmen

Eine Warteschlange lässt sich als doppelt verkettete, zyklische Liste implementieren.

Verkettete Listen

Wie bei allen Datenstrukturen, kann man für verkettete Listen mehr Operationen definieren und umsetzen, als ich hier aufliste. Eine gute Menge von Operationen wird durch das Java List Interface vorgegeben.

Einfach verkettete Liste

Sei $n$ die Anzahl der Elemente der Liste.

Operation	Worst-Case-Laufzeit	Anmerkungen
Suchen	${\cal O}(n)$	→ Element ist am Ende der Liste
Minimum	${\cal O}(n)$	→ Element ist am Ende der Liste
Maximum	${\cal O}(n)$	→ Element ist am Ende der Liste
Einfügen am Anfang	${\cal O}(1)$
Wahlfreies Einfügen	${\cal O}(n)$
Löschen	${\cal O}(n)$	→ Suchen
Vorgänger	${\cal O}(n)$
Nachfolger	${\cal O}(1)$

Doppelt verkettete Liste

Sei $n$ die Anzahl der Elemente der Liste.

Operation	Worst-Case-Laufzeit	Anmerkungen
Suchen	${\cal O}(n)$	→ Element ist am Ende der Liste
Minimum	${\cal O}(n)$	→ Element ist am Ende der Liste
Maximum	${\cal O}(n)$	→ Element ist am Ende der Liste
Einfügen am Anfang	${\cal O}(1)$
Wahlfreies Einfügen	${\cal O}(n)$
Löschen	${\cal O}(n)$	→ Suchen
Vorgänger	${\cal O}(1)$	Nur hier ist die doppelt-verkettete Liste besser als die einfach verkettete Liste.
Nachfolger	${\cal O}(1)$

Bäume

In der Vorlesung wurden Bäume sehr unpräzise eingeführt. Ich versuche das mal etwas präziser zu machen:

Sei $G = (V, E)$ ein gerichteter Graph. $G$ heißt gerichteter Baum $: \Leftrightarrow \exists_{r \in V} \forall_{x \in V}:$Es exisitert genau ein Pfad von $r$ nach $x$.

Sei $G = (V, E)$ ein gerichteter Baum und sei $r \in V$ das $r$ aus der Definition. $r$ heißt Wurzel von $G$.

ACHTUNG: Die folgende Definition habe ich mir ausgedacht! NICHT IN DER KLAUSUR VERWENDEN!

Sei $E \subseteq V \times V$ eine Menge ungerichteter Kanten. Dann bezeichne $G(E) := \{(v, w) | \{v, w\} \in E\}$ die Menge aller zugehörigen gerichteten Kanten.

Sei $U = (V, E)$ ein ungerichteter Graph. $U$ heißt ein ungerichteter Baum $:\Leftrightarrow \exists$ gerichteten Baum $G = (V, E')$ mit $E' \subsetneq G(E)$.

Sei $G = (V, E)$ ein Baum und $x, y \in V$. $x$ heißt Elternknoten von $y :\Leftrightarrow x$ liegt auf dem Pfad von der Wurzel nach $y$ direkt vor $y$.

Sei $G = (V, E)$ ein Baum und $x, y \in V$. $x$ heißt Kindknoten von $y :\Leftrightarrow y$ ist Elternknoten von $x$.

Binäre Bäume

Sei $G = (V, E)$ ein Baum. $G$ heißt binärer Baum $:\Leftrightarrow \forall_{x \in V}: x$ hat höchstens zwei Kindknoten.

Ich beziehe mich im folgenden auf ungerichtete, binäre Bäume. Soll heißen, jeder Knoten kennt seine Kinder- und seinen Vaterknoten.

Wie würde man das implementieren? Im Prinzip wie eine doppelt verkettete Liste. Jeder Knoten hat einen Zeiger auf den Eltern-Knoten und zwei Zeiger auf die Kindknoten.

Operation	Worst-Case-Laufzeit	Anmerkungen
Suchen	${\cal O}(\|V\| + \|E\|)$	→ Graphentraversierung
Minimum	${\cal O}(\|V\| + \|E\|)$	→ Graphentraversierung
Maximum	${\cal O}(\|V\| + \|E\|)$	→ Graphentraversierung
Einfügen	${\cal O}(\|V\|)$
Löschen	${\cal O}(\|V\| + \|E\|)$	→ Suchen
Vorgänger	${\cal O}(1)$	Implementierungsabhängig!
Nachfolger	${\cal O}(1)$

Suchbäume

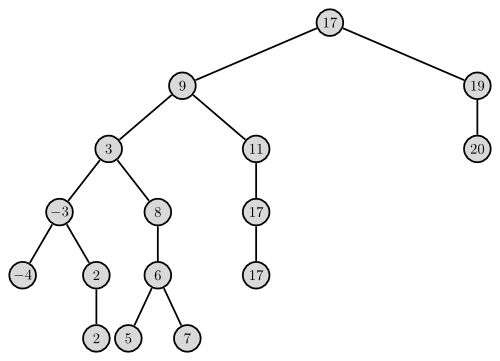
Dieser Baum hat die gleichen Werte wie der Baum oberhalb, aber es gilt nun: Der Wert aller Knoten links vom aktuellen Konten ist kleiner oder gleich dem des aktuelle, der Wert aller Knoten rechts davon ist echt größer.

Ich beschränke mich hier auf binäre Suchbäume.

Damit ergeben sich folgende Laufzeiten: Sei $G = (V, E)$ ein beliebiger binärer Suchbaum. Jeder Knoten kennt seine Kinder- und seinen Vaterknoten.

Operation	Worst-Case-Laufzeit	Anmerkungen
Suchen	${\cal O}(\|V\|)$	→ Verkettete Liste
Minimum	${\cal O}(\|V\|)$	→ Verkettete Liste
Maximum	${\cal O}(\|V\|)$	→ Verkettete Liste
Einfügen	${\cal O}(\|V\|)$	→ Verkettete Liste
Löschen	${\cal O}(\|V\|)$	→ Verkettete Liste
Vorgänger	${\cal O}(1)$	Implementierungsabhängig!
Nachfolger	${\cal O}(1)$

Rot-Schwarz-Bäume

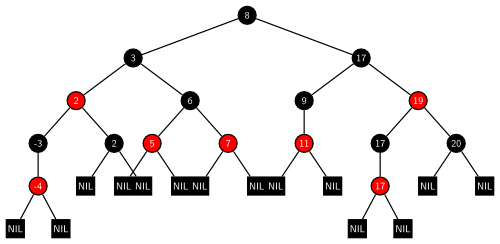
Sei $G = (V, E)$ ein binärer Suchbaum. G heißt Rot-Schwarz-Baum $: \Leftrightarrow$ Für G gilt:

Jeder Knoten ist entweder Rot oder Schwarz.
Der Wurzelknoten ist schwarz.
Die Blattknoten sind schwarz.
Ein Knoten ist rot $\Rightarrow$ Beide Kinder sind schwarz.
$\forall x \in V:$ Alle Pfade von x zu einem Blatt haben die gleiche Anzahl schwarzer Knoten.

Operation	Worst-Case-Laufzeit	Anmerkungen
Suchen	${\cal O}(\lg n)$
Minimum	${\cal O}(\lg n)$
Maximum	${\cal O}(\lg n)$
Einfügen	${\cal O}(\lg n)$
Löschen	${\cal O}(\lg n)$
Vorgänger	${\cal O}(1)$
Nachfolger	${\cal O}(1)$

Eine Python-Implementation ist hier zu finden: https://github.com/MartinThoma/algorithms

Heaps

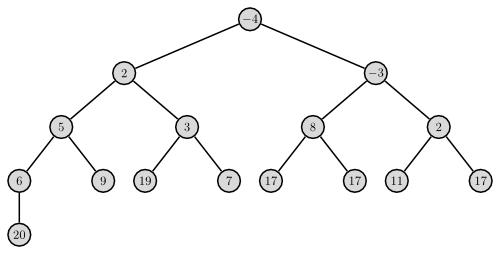
Ich beschränke mich im folgenden auf binäre Min-Heaps.

Operation	Worst-Case-Laufzeit	Anmerkungen
Suchen	${\cal O}(n)$	→ Falls als array dargestellt, einfach alle Elemente des Arrays durchlaufen
Minimum	${\cal O}(1)$
Extract-Minimum	${\cal O}(\log n)$	→ Heapify
Maximum	${\cal O}(n)$	→ Suche
Einfügen	${\cal O}(\log n)$	→ Heapify
Löschen	${\cal O}(\log n)$	→ Heapify (bei bekannter Position des Elements, sonst siehe Suche)
Vorgänger	${\cal O}(1)$	Hat keine besondere Bedeutung in Heaps.
Nachfolger	${\cal O} (1)$	Hat keine besondere Bedeutung in Heaps.

B-Bäume

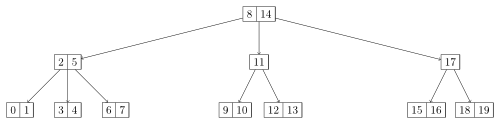
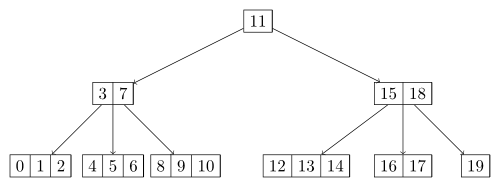
Ein B-Baum ist ein immer vollständig balancierter Baum, der Daten sortiert nach Schlüsseln speichert. Er kann binär sein, ist aber im Allgemeinen kein Binärbaum. Das Einfügen, Suchen und Löschen von Daten in B-Bäumen ist in amortisiert logarithmischer Zeit möglich. B-Bäume wachsen – und schrumpfen – anders als viele Suchbäume von den Blättern hin zur Wurzel.

Quelle: Wikipedia

Die beiden abgebildeten B-Bäume sind entstanden, indem die Zahlen von 0 bis 19 in aufsteigener Reihenfolge eingefügt wurden.

Für einen B-Baum der Ordnung t, $t \geq 2$, gilt:

Alle Pfade von der Wurzel zu einem Blatt sind gleich lang.
Die Wurzel hat mindestens 2, höchstens 2t Kinder.
Alle anderen inneren Knoten haben mindestens t, höchstens 2t Kinder.
Jeder Knoten mit i Kindern hat i-1 Schlüssel.

Die beiden B-Bäume habe ich mit diesem Script erstellt.

Mehr zu B-Bäumen gibt es in diesem Artikel über B-Bäume.

Tries

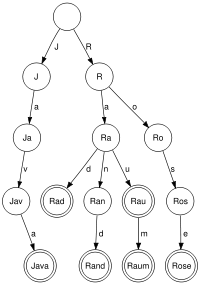
Bildquelle: Wikipedia

Ein Trie ist ein spezieller digitaler Baum.

Ein Trie oder Präfixbaum ist eine Datenstruktur, die in der Informatik zum Suchen nach Zeichenketten verwendet wird. Es handelt sich dabei um einen speziellen Suchbaum zur gleichzeitigen Speicherung mehrerer Zeichenketten.