Die euklidische Normalform einer linearen Isometrie, manchmal auch lineare Normalform gennant, hat folgende Gestalt:
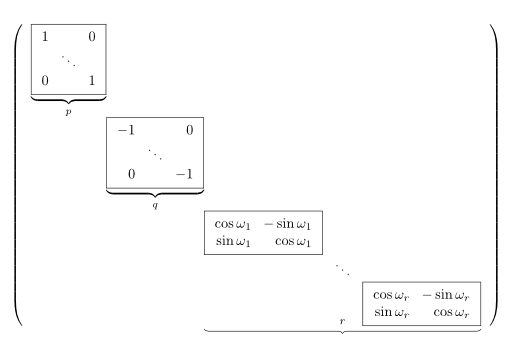
Bei einer $n \times n$-Matrix gilt also folgende Gleichung: $n = p + q + 2r$
Bestimmung der Normalform
Sei $\Phi$ eine lineare Isometrie eines euklidischen Vektorraumes. Dann habe $\Phi$ die Abbildungsmatrix $A$. Sei $B := A + A^T$. Wenn man die euklidische Normalform bilden will, bestimmt man zuerst das charakteristische Polynom von $B$. Die Nullstellen davon sind die Eigenwerte. Die algebraische Vielfachheit des Eigenwertes 2 von $B$ (die Potenz im charakteristischen Polynom) gibt die Anzahl der 1er an, genauso gibt die Vielfachheit des Eigenwertes -2 die Anzahl der -1er an.
Die restlichen Eigenwerte $\lambda_1, \dots, \lambda_r$ geben die Drehkästchen an.
Es gilt: $\cos \omega = \frac{\lambda}{2}$ $\sin \omega = \sqrt{1 - \frac{\lambda^2}{4}}$
Mit diesen Angaben kann man direkt die euklidische Normalform angeben.
Bestimmung der Transformationsmatrix
Eigenräume bestimmen
Die Eigenräume berechnet man wie gewohnt:
$\text{Eig}(\lambda_i) = \text{Kern}(B- \lambda_i \cdot E)$
ONB bestimmen
Nun wählt man für jeden Eigenraum eine Basis Orthonormalbasis aus Eigenvektoren. Das kann man mit dem Gram-Schmidtsches Orthogonalisierungsverfahren machen, also: Wähle ein beliebiges $w_1 \in \text{Eig}(\lambda_i)$.
Quellen
- Skript von Prof. Dr. Leuzinger, S. 228 ff.
- Klausur „Lineare Algebra und analytische Geometrie“ vom Frühjahr 2007, Aufgabe II.4