Calculate square roots

Suppose you have an equation like this:

$x^2 = a, \;\;\;\; a \in \mathbb{R}_{\geq 0}$

Your task is to compute the solution $x \in \mathbb{R}_{\geq 0}$.

How do you solve this algorithmically?

Input and output

Write a program that takes two parameters $a, n \in \mathbb{N}_{\geq 1}$:

$a$: The number you should take the square root of. $a$ is not bigger than 65535. To make this a little bit simpler, you can also assume that $a$ is an integer.
$n$: Number of iterations you may use

Your program should output exactly one positive floating point number. The decimal separator is a point. At the end of the number should be a newline character \n.

Reference code

// Thanks to http://stackoverflow.com/a/15363123/562769
#include <stdio.h>
#include <gmp.h>

int main(int argc, char *argv[]) {
    mpf_t res, a;
    mpf_set_default_prec(1000000); // Increase this number.
    mpf_init(res);
    mpf_init(a);
    mpf_set_str(a, "2", 10);
    mpf_sqrt (res, a);
    gmp_printf("%.1000Ff\n\n", res); // Increase this number.
    return 0;
}

You need GMP (libgmp-dev) to compile this.

Compile it like this:

gcc sqrt-reference.c  -lgmp -lm -O0 -g3 -o reference.out

This is the script I use to get the number of correct digits:

#!/usr/bin/env python
# -*- coding: utf-8 -*-


def getScore(program, a, n):
    import os

    os.system("./reference.out " + str(a) + " > reference.txt")
    os.system("./" + program + " " + str(a) + " " + str(n) + " > result.txt")

    f = open("reference.txt", "r")
    reference = f.read()
    f.close()

    f = open("result.txt", "r")
    result = f.read()
    f.close()

    points = 0
    areEqual = True
    while reference[points] != "\n" and result[points] != "\n":
        if reference[points] == result[points]:
            points += 1
        else:
            break
    if points >= 2:
        points -= 1  # decimal point
    return points


if __name__ == "__main__":
    from argparse import ArgumentParser

    parser = ArgumentParser()

    # Add more options if you like
    parser.add_argument(
        "-p",
        "--program",
        dest="program",
        help="your program",
        metavar="FILE",
        required=True,
    )
    parser.add_argument(
        "-a", metavar="A", type=int, required=True, help="calculate squre root of a"
    )
    parser.add_argument(
        "-n", metavar="N", type=int, required=True, help="maximum n iterations"
    )

    args = parser.parse_args()

print(
    "Points for a=%i and n=%i: %i"
    % (args.a, args.n, getScore(args.program, args.a, args.n))
)

Newton's method

How should be choose the initial value? I thought $\frac{a}{2}$ could be ok. In a good implementation you'll probably do this with a lookup table.

With long double:

#include <iostream>
#include <cmath>

using namespace std;

long double newton(int a, int n) {
    long double x = ((long double)a)/2;
    for (int i=0; i<n; i++) {
        x = x - (x*x - a)/(2*x);
    }
    return x;
}

int main(int argc, char *argv[]) {
    if (argc != 3) {
        cout << "Please enter exactly two arguments." << endl;
        return 1;
    }
    int a = atoi(argv[1]);
    int n = atoi(argv[2]);
    printf("%.80Lf\n", newton(a, n));
    return 0;
}

I failed to convert this to a version that uses GMP :-/

But it converges quite fast:

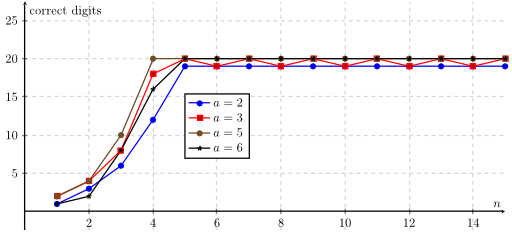
Newtons method for calculating square roots

Exponential identity

According to Wikipedia (Source: Methods of computing square roots) many calculators use the following identity:

$\displaystyle \sqrt{a} = e^{\frac{1}{2}\ln a}$

But to calculate this, you need to be able to calculate $e^x$ for $x \in \mathbb{R}_{\geq 0}$ and $\ln(a)$ for $a \in \mathbb{R}_{\geq 0}$.

I've used the definition of $e^x$ to calculate $e^x$: $\displaystyle e^x := \sum_{i = 0}^\infty \frac{x^i}{i!}$

and:

$\displaystyle \ln(1+x) =- \sum_{k=0}^\infty \frac{(-x)^{k+1}}{k+1}$

So I gave it a try:

#include <iostream>
#include <cmath>

using namespace std;

long double ln(int S, int n) {
    long double tmp = S - 1;
    long double result = tmp;
    long double sign = 1.0;
    for (int i=2; i<n/2; i++) {
        tmp *= (S-1);
        sign *= -1;
        result += sign*tmp/i;
    }
    return result;
}

long double e(long double x, int n) {
    long double numerator = 1;
    long double denominator = 1;
    long double result = 1;
    for (int i=1; i<n/2; i++) {
        numerator *= x;
        denominator *= i;
        result += numerator/denominator;
    }
    return result;
}

long double sqrt(int a, int n) {
    return e(ln(a, n)*0.5, n);
}

int main(int argc, char *argv[]) {
    if (argc != 3) {
        cout << "Please enter exactly two arguments." << endl;
        return 1;
    }
    int a = atoi(argv[1]);
    int n = atoi(argv[2]);
    printf("%.80Lf\n", sqrt(a, n));
    return 0;
}

This converges VERY slow: For $a = 2$

$n=1$: 1 digit correct
$n=10$: 1 digit correct
$n=100$: 2 digits correct
$n=1000$: 4 digit correct
$n=10,000$: 5 digit correct
$n=100,000$: 5 digit correct
$n=1,000,000$: 6 digit correct

Ok, lets take a better Taylor series for calculating $e^x$: $\displaystyle e^x = \sum_{k=0}^\infty \frac{x^{-1+2 k} (2 \cdot k+x)}{(2\cdot k)!}$

This didn't change anything! I'm very surprised ... as I've calculated $\pi$ for another article, changing the series to something similar improved the speed of convergence drastically.

Calculate square roots

Input and output

Reference code

Newton's method

Exponential identity

See also

Published

Category

Tags

Contact