Explaining away is an effect where which is explained in Pearl (1988) with an example similar to the following one:
A car's engine can fail (\(X\)). The reason might either be a dead battery \(Y\) or a blocked fuel pump \(Z\).
This results in the following Bayesian Network:
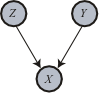
Now assume you know that the engine does not fail (\(X=0\)). This guarantees that the battery is not dead (\(Y=0\)) and the fuel pump is not blocked (\(Z=0\)).
However, if the engine failed (\(X=1\)) it gets more interesting. Let's say the engine works with a probability of 90%. From the graph, you can see that we assume that a dead battery is independant of a blocked fuel pump. Let's also assume that you know that either the fuel pump is blocked or the battery is dead when the engine failed. There is no other option.
This makes setting the probability distribution up interesting. There is still 10% left which has to be distributed amongst \(P(X=1,Y=1,Z=1), P(X=1,Y=1,Z=0), P(X=1,Y=0,Z=1)\):
| X | Y | Z | P(X,Y,Z) | comment |
|---|---|---|---|---|
| 0 | 0 | 0 | 0.9 | Engine works |
| 0 | 0 | 1 | 0 | impossible - blocked fuel pump and working engine |
| 0 | 1 | 0 | 0 | impossible - dead battery and working engine |
| 0 | 1 | 1 | 0 | impossible - dead battery, blocked fuel pump and working engine |
| 1 | 0 | 0 | 0 | impossible - a cause we don't have in our graph |
| 1 | 0 | 1 | a | |
| 1 | 1 | 0 | b | |
| 1 | 1 | 1 | c |
However, if you assume that \(Y\) and \(Z\) are independent, given \(X\), then you would have to set \(P(Y=0, Z=0|X=1) = P(Y=0|X=1) \cdot P(Z=0|X=1)\) which would not be 0 except one of the probabilities would be 0. Or, putting it different again: Given that you know the engine is broken, the event of a dead battery and a blocked fuel pump are suddenly not independent anymore!
What does it mean
This does not mean there is "suddenly" a causatal connection between a dead battery and a blocked fuel pump. It only means you can learn something for your predictions.