How to create UML class diagrams

Dia

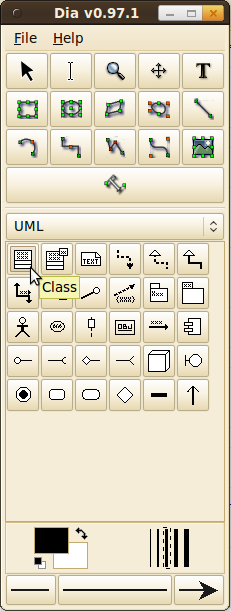
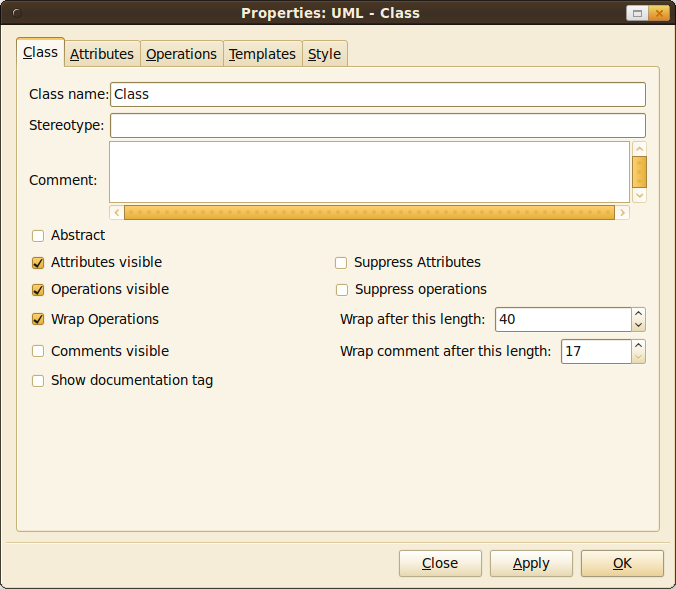
Creating UML diagrams with Dia works like a charm! It provides some default tools. You should simply try it. Dia is a free tool.

Take a look at these screenshots:

LaTeX

I only know MetaUML for creating class diagrams entirely in LaTeX. Does anybody know something different?

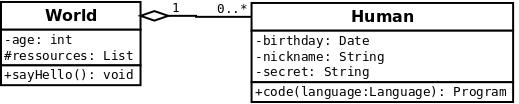
Of course, you can include a diagram created with Dia:

1. Export the diagram as PNG (antialized)
2. Add something like that to your tex-file: \includegraphics[width=180mm]{myDiagramm.png}

MetaUML

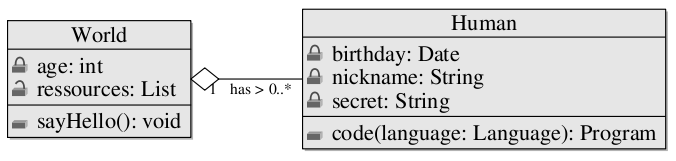
A MetaUML class diagram looks like that in code (saved as myMetaDiagram.mp):

input metauml;
beginfig(1);
    Class.World("World")
           ("-age: int",
            "#ressources: List")
           ("+sayHello(): void");

    Class.NoHuman("Human")
           ("-birthday: Date",
            "-nickname: String",
            "-secret: String")
           ("+code(language: Language): Program");

    leftToRight(50)(World, NoHuman);
    drawObjects(World, NoHuman);

    link(aggregation)(NoHuman.w -- World.e);
    item(iAssoc)("1")(obj.n     = .2[World.e,NoHuman.w]);
    item(iAssoc)("has >")(obj.n = .5[World.e,NoHuman.w]);
    item(iAssoc)("0..*")(obj.n  = .8[World.e,NoHuman.w]);

endfig;
end

You have to execute mpost before you can compile LaTeX. A working example is in this UML Archive.

It looks like that in your generated PDF file:

See also

• Wikipedia: Class diagram, Dia
• Dia: Dia und UML
• MetaUML: Tutorial, Reference and Test Suite
• Freies Magazin, Mai 2012: Astah – Kurzvorstellung des UML-Programms (German)