How to draw speech bubbles

The nice icon is from Wikipedia Commons and part of the Crystal Clear project by Everaldo Coelho.

Preparation

1. Install inkscape.
2. Get an image where you want to put the speech bubble.
3. Add text with F2

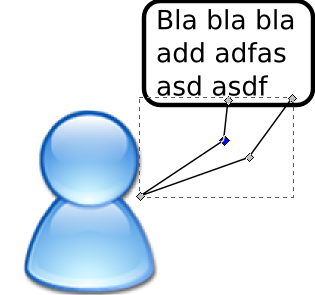
Now it should looke like this:

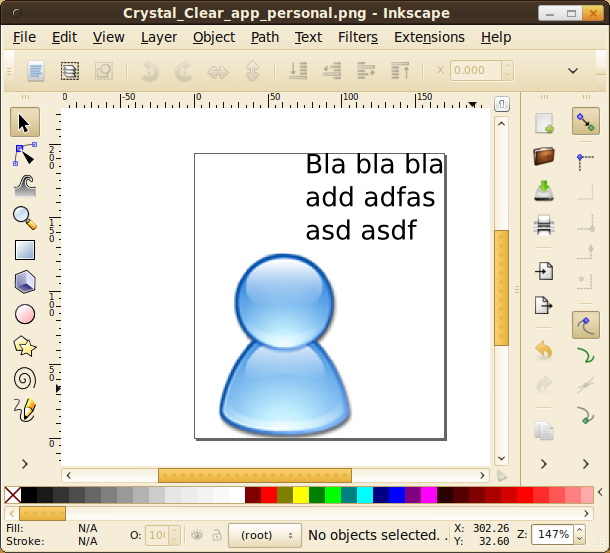
Rectangle

Now you have to put a rectangle (F2) or an ellipses (F5) around your text. The rectangle should be placed below the text (Page down).

To make positioning easier, group the text and the surrounding box:

1. Mark box by clicking on it
2. Shift + Click on the text
3. Group with Ctrl + G

Now it should looke like this:

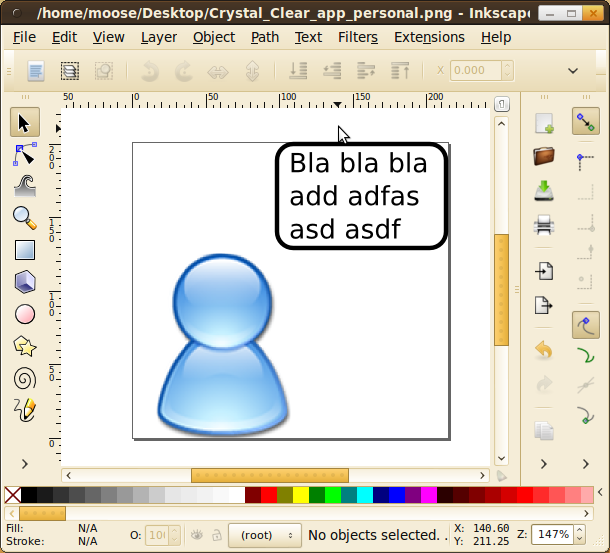
Indicator

To add the "indicator" that shows who spoke, press Shift + F6 and add a triangle that overlaps with the box:

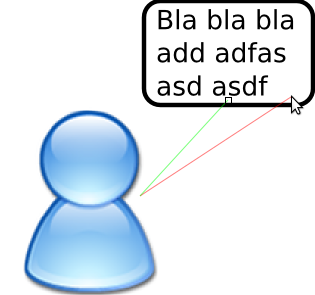
Then press F2 to modify the path by nodes. Add some controll nodes in between by double-clicking on the path in between:

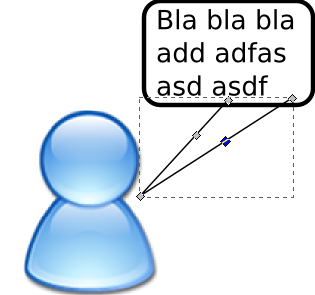
Then delete them. Now you have those round curves that can be manipulated with the little circles: