Jordansche Normalform: 2x2 Matrizen

Hier sind $2 \times 2$ Beispiele zum Hauptartikel Wie berechnet man die Jordan’sche Normalform?.

Beispiel 1

Gegeben sei die Matrix \(A \in \mathbb{R}^{2 \times 2}\):

$$A := \begin{pmatrix} 11 & -4\\ 25 & -9 \end{pmatrix}$$

.

Jordannormalform bestimmen

1. Charakteristisches Polynom berechnen: \(p_A(\lambda) = (\lambda - 1)^2\).

Daraus folgt: \(\lambda = 1\) ist einziger Eigenwert \(\Rightarrow\) 1 Jordanblock

2. Anzahl der Jordankästchen bestimmen:

\begin{align} \dim E_{1} &= \dim \text{Kern}(A -1 \cdot I) \\ &= \dim \text{Kern} \begin{pmatrix} 10 & -4\\ 25 & -10 \end{pmatrix}\\ &= \dim \text{Kern} \begin{pmatrix} 10 & -4\\ 0 & 0 \end{pmatrix}\\ &= \dim \left [ \begin{pmatrix}2\\5\end{pmatrix} \right ] \\ &= 1 \end{align}

\(\Rightarrow\) es gibt genau 1 Jordankästchen in diesem Jordanblock.

$$\Rightarrow J = \begin{pmatrix}1 & 1\\ 0 & 1 \end{pmatrix}$$

.

Basiswechselmatrix bestimmen

Basisvektoren für den Eigenwert 1 bestimmen:

$$\Omega = \Phi_{| H_\lambda} - \lambda \cdot id = \begin{pmatrix} 10 & - 4\\ 25 & -10 \end{pmatrix} $$

,

$$K_1 = \text{Kern } \Omega^1 = \left [ \begin{pmatrix}2 \\ 5 \end{pmatrix} \right ]$$
$$K_2 = \text{Kern } \Omega^2 = \text{Kern } (\begin{pmatrix}10 & -4\\ 25 & -10 \end{pmatrix} \cdot \begin{pmatrix}10 & -4\\ 25 & -10 \end{pmatrix}) = \text{Kern } (\begin{pmatrix}0 & 0\\ 0 & 0 \end{pmatrix}) = \left[ \begin{pmatrix}1 \\ 0 \end{pmatrix}, \begin{pmatrix}0 \\ 1 \end{pmatrix} \right]$$
$$K_2 \stackrel{!}{=} U_1 \oplus K_1 \Rightarrow \left [ \begin{pmatrix} 1 \\ 0 \end{pmatrix} \right ] ~~~ U_0 = K_1$$
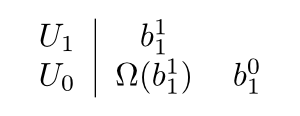
Schema zum finden der Basiswechselmatrix
Schema zum finden der Basiswechselmatrix

Wähle

$$b_1^1 \in U_1: b_1^1 = \begin{pmatrix}1 \\0 \end{pmatrix} \Rightarrow \Omega(b_1^1) = \begin{pmatrix}10 \\ 25 \end{pmatrix}$$
$$\Rightarrow S = \begin{pmatrix} 10 & 1 \\ 25 & 0 \end{pmatrix}$$
$$\Rightarrow S^{-1} = \begin{pmatrix} 0 & \frac{1}{25} \\ 1 & -\frac{2}{5} \end{pmatrix}$$
$$A = S \cdot J \cdot S^{-1}$$
$$\Leftrightarrow \begin{pmatrix} 11 & -4\\ 25 & -9 \end{pmatrix} = \begin{pmatrix} 10 & 1 \\ 25 & 0 \end{pmatrix} \cdot \begin{pmatrix}1 & 1\\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 0 & \frac{1}{25} \\ 1 & -\frac{2}{5} \end{pmatrix}$$

Beispiel 2

Gegeben sei die Matrix \(A \in \mathbb{R}^{2 \times 2}\):

$$A := \begin{pmatrix} 1 & 2\\ 3 & 6 \end{pmatrix}$$

.

Jordannormalform bestimmen

1. Charakteristisches Polynom berechnen:

$$p_A(\lambda) = \det \begin{pmatrix} 1 -\lambda & 2\\ 3 & 6 - \lambda \end{pmatrix} = (1- \lambda) \cdot (6 - \lambda) - 6 = 6-6\lambda-\lambda+\lambda^2-6=\lambda^2-7\lambda = \lambda \cdot (\lambda - 7)$$

Daraus folgt: 0 und 1 sind Eigenwerte. Sie haben jeweils die algebraischen Vielfachheit 1. Daraus folgt: Die Jordansche Normalform hat genau zwei Jordanblöcke, die beide die Größe 1x1 haben. Daraus folgt: Beide Jordanblöcke haben genau ein Jordankästchen der Größe 1x1. Daraus folgt: Die Jordansche Normalform der Matrix ist:

$$J = \begin{pmatrix} 0 & 0\\ 0 & 7 \end{pmatrix}$$

Basiswechselmatrix bestimmen

Basisvektoren für den Eigenwert 0 bestimmen:

$$K_1 = \text{Kern }(A- 0 \cdot E) = \text{Kern } \begin{pmatrix} 1 & 2\\ 3 & 6 \end{pmatrix} = \left [ \begin{pmatrix}2 \\ -1 \end{pmatrix} \right ] $$

Basisvektoren für den Eigenwert 7 bestimmen:

$$K_1 = \text{Kern }(A- 7 \cdot E) = \text{Kern } \begin{pmatrix} -6 & 2\\ 3 & -1 \end{pmatrix} = \text{Kern } \begin{pmatrix} 1 & -\frac{1}{3}\\ 0 & 0 \end{pmatrix} = \left [ \begin{pmatrix}1 \\ 3 \end{pmatrix} \right ] $$

Zusammensetzen:

$$S = \begin{pmatrix}2 & 1 \\ -1 & 3 \end{pmatrix}$$
$$S^{-1} = \frac{1}{7} \cdot \begin{pmatrix}3 & -1 \\ 1 & 2 \end{pmatrix}$$

Anmerkung

Man hätte übrigens jeden Vektor aus

$$\left [ \begin{pmatrix}2 \\ -1 \end{pmatrix} \right ]$$

nehmen können. Angenommen, man hätte den Vektor

$$\begin{pmatrix}-14 \\ 7 \end{pmatrix}$$

gewählt:

$$S = \begin{pmatrix}-14 & 1 \\ 7 & 3 \end{pmatrix}$$
$$S^{-1} = \frac{1}{49} \cdot \begin{pmatrix}-3 & 1 \\ 7 & 14 \end{pmatrix}$$

Das gleiche gilt natürlich für jeden anderen gewählten Vektor. Die inverse Matrix ändert sich selbstverständlich, jedoch nicht die Jordansche Normalform oder die ursprüngliche Matrix.

Published


by

Category

German posts

Tags

Contact