This post is about simple implementations of matrix multiplications. The goal of this post is to find out how easy it is to implement a matrix multiplication in Python, Java and C++. Additionally, I want to get to know how good these solutions are.
The second post will be an implementation of the Strassen algorithm for matrix multiplication. Strassen algorithm does matrix multiplication in \(\cal O(n^{log_2(7)+o(1)}) \approx \cal O(n^{2.807})\) instead of \(\cal O(n^3)\). I am quite sure this will outperform almost every other change. See Part II: The Strassen algorithm in Python, Java and C++.
The third post will be about parallel programming. I have two cores and I want to see if it will be significantly faster if I use both of them.
The implementations
I will post all scripts for this test and I've added a GIT repository, so feel free to test it on your machine. I am also happy if you post some of your solutions with running times ☺ I am quite sure that my Java and C++ code can be written much better. If you know how, please leave a comment. If you know other languages, you could create a script for these. I focus on Python, Java and C++ as they are very often used.
I have implemented these three types of algorithms for this post:
- ijk-algorithm: This is a simple, straight forward implementation of a matrix multiplication. I've used the definition of matrix multiplication. I didn't use multiple threads.
- ikj-algorithm: just like the ijk-algorithm, but I've switched two of the three the for-loops.
- Library-functions: I always prefer libraries over self-implemented solutions. I think they are faster than anything I could come up with in a reasonable amount of time.
If you post a solution, please consider these restrictions:
- Input: The input file should get passed with the parameter
-i, e.g.:python -i 2000.inorjava Shell -i 2000.in - The standard value for the command line parameter -i should be "2000.in" (a $2000 \times 2000$ matrix)
- The user should not have to give the size of the matrix!
- The two square-matrices that should get multiplied are ...
- ... read from a text-file.
- ... represented like this:
- Every line of one matrix is one line in the text-file.
- Newlines are only "\n".
- Every number is separated by "\t".
- The both matrices are separated by one newline.
- Output: The result has to get printed to standard output.
- The result has to be formatted like the input (tabs for separation of number, \n for marks a new line)
The Tests
I will check the speed of a multiplication of two big matrices following for Python, Java and C++ for all algorithms like this:
$ time python scriptABC.py -i ../2000.in > result.txt
$ diff result.txt bigMatrix.out
The bigMatrix.out was produced by the Python ijk-implementation. I make the diff to test if the result is correct.
The Setting
I created two "random" matrices \(A, B \in \mathbb{N}^{2000 \times 2000}\) with this script. The file that was created needs about 29.7 MB and is also in the GIT-Hub repository. But you can also create the matrices with this script:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import random
random.seed(1234)
def createRandomMatrix(n):
maxVal = 1000 # I don't want to get Java / C++ into trouble
matrix = []
for i in range(n):
matrix.append([random.randint(0, maxVal) for el in range(n)])
return matrix
def saveMatrix(matrixA, matrixB, filename):
f = open(filename, "w")
for i, matrix in enumerate([matrixA, matrixB]):
if i != 0:
f.write("\n")
for line in matrix:
f.write("\t".join(map(str, line)) + "\n")
n = 3
matrixA = createRandomMatrix(n)
matrixB = createRandomMatrix(n)
saveMatrix(matrixA, matrixB, "2000.in")
All scripts are tested on my computer:
| Acer TravelMate 5735Z | |
| CPU | 2x Pentium(R) Dual-Core CPU T4500 @2.30GHz |
| RAM | 4 GB |
| Video Card | Intel GMA 4500MHD |
| System | Ubuntu 10.10.04 LTS |
Python
I've used Python 2.6.5.
ijk-algorithm
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from optparse import OptionParser
parser = OptionParser()
parser.add_option(
"-i",
dest="filename",
default="2000.in",
help="input file with two matrices",
metavar="FILE",
)
(options, args) = parser.parse_args()
def read(filename):
lines = open(filename, "r").read().splitlines()
A = []
B = []
matrix = A
for line in lines:
if line != "":
matrix.append(map(int, line.split("\t")))
else:
matrix = B
return A, B
def printMatrix(matrix):
for line in matrix:
print("\t".join(map(str, line)))
def standardMatrixProduct(A, B):
n = len(A)
C = [[0 for i in range(n)] for j in range(n)]
for i in range(n):
for j in range(n):
for k in range(n):
C[i][j] += A[i][k] * B[k][j]
return C
A, B = read(options.filename)
C = standardMatrixProduct(A, B)
printMatrix(C)
real 56m49.266s
user 56m30.524s
sys 0m2.980s
ikj-algorithm
def ikjMatrixProduct(A, B):
n = len(A)
C = [[0 for i in range(n)] for j in range(n)]
for i in range(n):
for k in range(n):
for j in range(n):
C[i][j] += A[i][k] * B[k][j]
return C
real 44m36.507s
user 44m13.458s
sys 0m2.000s
Psyco ikj-algorithm
Psyco is a just in time compiler, which makes my scripts MUCH faster. It is very simple to use. Add these two lines at the top of the ikj-script:
import psyco
psyco.full()
real 6m14.820s
user 6m12.959s
sys 0m0.620s
Amazing, isn't it?
Libraries
NumPy
NumPy-Version: 1.3.0 (Current version is 1.6.2, see Wiki)
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy
from optparse import OptionParser
parser = OptionParser()
parser.add_option(
"-i",
dest="filename",
default="2000.in",
help="input file with two matrices",
metavar="FILE",
)
(options, args) = parser.parse_args()
def read(filename):
lines = open(filename, "r").read().splitlines()
A = []
B = []
matrix = A
for line in lines:
if line != "":
matrix.append(map(int, line.split("\t")))
else:
matrix = B
return A, B
def printMatrix(matrix):
matrix = numpy.array(matrix)
for line in matrix:
print("\t".join(map(str, line)))
A, B = read(options.filename)
A = numpy.matrix(A)
B = numpy.matrix(B)
C = A * B # easy and intuitive, isn't it?
printMatrix(C)
real 1m38.425s
user 1m36.066s
sys 0m0.520s
SciPy
You might need to install python-scitools.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy
import scipy
from optparse import OptionParser
parser = OptionParser()
parser.add_option(
"-i",
dest="filename",
default="2000.in",
help="input file with two matrices",
metavar="FILE",
)
(options, args) = parser.parse_args()
def read(filename):
lines = open(filename, "r").read().splitlines()
A = []
B = []
matrix = A
for line in lines:
if line != "":
matrix.append(map(int, line.split("\t")))
else:
matrix = B
return A, B
def printMatrix(matrix):
matrix = numpy.array(matrix)
for line in matrix:
print("\t".join(map(str, line)))
A, B = read(options.filename)
A = scipy.matrix(A)
B = scipy.matrix(B)
C = A * B # easy and intuitive, isn't it?
printMatrix(C)
real 1m35.795s
user 1m33.438s
sys 0m0.488s
Conclusion for Python
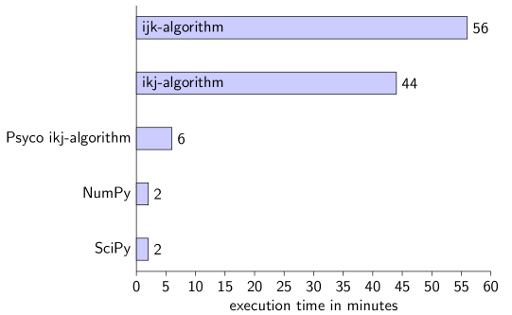
Using NumPy is by far the easiest and fastest option. I've needed about five minutes for each of the non-library scripts and about 10 minutes for the NumPy/SciPy scripts.
By the way, it is useless to combine Psyco and NumPy. It gets a little bit faster (1 minute and 28 seconds), but this could also be a random effect. If you execute it many times, you will see that the execution time is never the same.
Java
I am using this Java version:
$ java -version
java version "1.6.0_20"
OpenJDK Runtime Environment (IcedTea6 1.9.13) (6b20-1.9.13-0ubuntu1~10.04.1)
OpenJDK Server VM (build 19.0-b09, mixed mode)
ijk-algorithm
import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;
import java.util.LinkedList;
import java.util.List;
import java.util.ArrayList;
public class Shell {
static List<ArrayList<ArrayList<Integer>>> read(String filename) {
ArrayList<ArrayList<Integer>> A = new ArrayList<ArrayList<Integer>>();
ArrayList<ArrayList<Integer>> B = new ArrayList<ArrayList<Integer>>();
String thisLine;
try {
BufferedReader br = new BufferedReader(
new FileReader(filename));
// Begin reading A
while ((thisLine = br.readLine()) != null) {
if (thisLine.trim().equals("")) {
break;
} else {
ArrayList<Integer> line = new ArrayList<Integer>();
String[] lineArray = thisLine.split("\t");
for (String number : lineArray) {
line.add(Integer.parseInt(number));
}
A.add(line);
}
}
// Begin reading B
while ((thisLine = br.readLine()) != null) {
ArrayList<Integer> line = new ArrayList<Integer>();
String[] lineArray = thisLine.split("\t");
for (String number : lineArray) {
line.add(Integer.parseInt(number));
}
B.add(line);
}
br.close();
} catch (IOException e) {
System.err.println("Error: " + e);
}
List<ArrayList<ArrayList<Integer>>> res = new LinkedList<ArrayList<ArrayList<Integer>>>();
res.add(A);
res.add(B);
return res;
}
static int[][] ijkAlgorithm(ArrayList<ArrayList<Integer>> A,
ArrayList<ArrayList<Integer>> B) {
int n = A.size();
// initialise C
int[][] C = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
C[i][j] += A.get(i).get(k) * B.get(k).get(j);
}
}
}
return C;
}
static void printMatrix(int[][] matrix) {
for (int[] line : matrix) {
int i = 0;
StringBuilder sb = new StringBuilder(matrix.length);
for (int number : line) {
if (i != 0) {
sb.append("\t");
} else {
i++;
}
sb.append(number);
}
System.out.println(sb.toString());
}
}
public static void main(String[] args) {
String filename;
if (args.length < 2) {
filename = "2000.in";
} else {
filename = args[1];
}
List<ArrayList<ArrayList<Integer>>> matrices = read(filename);
ArrayList<ArrayList<Integer>> A = matrices.get(0);
ArrayList<ArrayList<Integer>> B = matrices.get(1);
int[][] C = ijkAlgorithm(A, B);
printMatrix(C);
}
}
real 27m21.295s
user 26m53.877s
sys 0m4.368s
Note: Java is not C++! If you use Vector instead of ArrayList, you get these results:
real 82m26.754s
user 80m42.003s
sys 0m24.598s
One reason might be that Vector is synchronized.
ikj-algoirthm
I've only switched line 60 and line 61.
real 2m9.478s
user 1m26.369s
sys 0m39.162s
Library: JAMA
I've searched in Google for "java matrix multiplication". The first 10 results were only implementations of the ijk-algorithm. Although the ijk-algorithm is very easy, most of the results were only questions where people tried to implement it.
After some search (20 minutes minimum) I've found JAMA. They also have a documentation. You might need to install this for the following code:
sudo apt-get install libjama-*
import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import Jama.Matrix;
public class Shell {
static List<ArrayList<ArrayList<Double>>> read(String filename) {
ArrayList<ArrayList<Double>> A = new ArrayList<ArrayList<Double>>();
ArrayList<ArrayList<Double>> B = new ArrayList<ArrayList<Double>>();
String thisLine;
try {
BufferedReader br = new BufferedReader(new FileReader(filename));
// Begin reading A
while ((thisLine = br.readLine()) != null) {
if (thisLine.trim().equals("")) {
break;
} else {
ArrayList<Double> line = new ArrayList<Double>();
String[] lineArray = thisLine.split("\t");
for (String number : lineArray) {
line.add((double) Integer.parseInt(number));
}
A.add(line);
}
}
// Begin reading B
while ((thisLine = br.readLine()) != null) {
ArrayList<Double> line = new ArrayList<Double>();
String[] lineArray = thisLine.split("\t");
for (String number : lineArray) {
line.add((double) Integer.parseInt(number));
}
B.add(line);
}
} catch (IOException e) {
System.err.println("Error: " + e);
}
List<ArrayList<ArrayList<Double>>> res = new LinkedList<ArrayList<ArrayList<Double>>>();
res.add(A);
res.add(B);
return res;
}
static int[][] ijkAlgorithm(ArrayList<ArrayList<Integer>> A,
ArrayList<ArrayList<Integer>> B) {
int n = A.size();
// initialise C
int[][] C = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
C[i][j] += A.get(i).get(k) * B.get(k).get(j);
}
}
}
return C;
}
static void printMatrix(Matrix matrix, int n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (j != 0) {
System.out.print("\t");
}
System.out.printf("%.0f", matrix.get(i, j));
}
System.out.println("");
}
}
public static void main(String[] args) {
String filename;
if (args.length < 2) {
filename = "2000.in";
} else {
filename = args[1];
}
List<ArrayList<ArrayList<Double>>> matrices = read(filename);
ArrayList<ArrayList<Double>> A = matrices.get(0);
ArrayList<ArrayList<Double>> B = matrices.get(1);
int n = A.size();
double[][] Aarray = new double[n][n];
double[][] Barray = new double[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
Aarray[i][j] = A.get(i).get(j);
Barray[i][j] = B.get(i).get(j);
}
}
Matrix AM = new Matrix(Aarray);
Matrix BM = new Matrix(Aarray);
Matrix CM = AM.times(BM);
printMatrix(CM, n);
}
}
real 1m36.506s
user 0m51.367s
sys 0m45.043s
It took me about two hours to get it work. I had to add the JAMA-JAR to eclipse, export my project as a JAR and run it with
$ time java -jar jama-shell.jar -i ../2000.in > jama-result.out
I still have no idea how to compile it with bash only.
Conclusion for Java
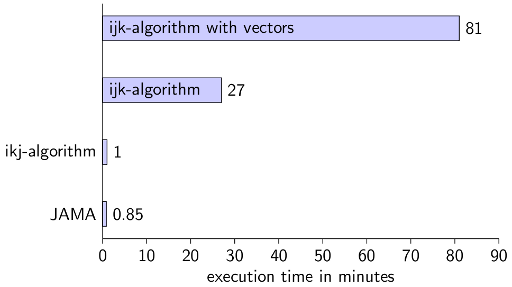
You should definitely know if some Java-datastructures are synchronised or not. And you should know how the computer / caches work.
C++
I have gcc 4.4.3 and compiled everything with these options:
$ g++ -std=c++98 -Wall -O3 -g myScript.cpp -o $(PROBLEM).out -pedantic
ijk-algorithm
#include <sstream>
#include <string>
#include <fstream>
#include <iostream>
#include <vector>
using namespace std;
struct Result {
vector< vector<int> > A;
vector< vector<int> > B;
};
Result read(string filename) {
vector< vector<int> > A, B;
Result ab;
string line;
ifstream infile;
infile.open (filename.c_str());
int i = 0;
while (getline(infile, line) && !line.empty()) {
istringstream iss(line);
A.resize(A.size() + 1);
int a, j = 0;
while (iss >> a) {
A[i].push_back(a);
j++;
}
i++;
}
i = 0;
while (getline(infile, line)) {
istringstream iss(line);
B.resize(B.size() + 1);
int a;
int j = 0;
while (iss >> a) {
B[i].push_back(a);
j++;
}
i++;
}
infile.close();
ab.A = A;
ab.B = B;
return ab;
}
vector< vector<int> > ijkalgorithm(vector< vector<int> > A,
vector< vector<int> > B) {
int n = A.size();
// initialise C with 0s
vector<int> tmp(n, 0);
vector< vector<int> > C(n, tmp);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
return C;
}
void printMatrix(vector< vector<int> > matrix) {
vector< vector<int> >::iterator it;
vector<int>::iterator inner;
for (it=matrix.begin(); it != matrix.end(); it++) {
for (inner = it->begin(); inner != it->end(); inner++) {
cout << *inner;
if(inner+1 != it->end()) {
cout << "\t";
}
}
cout << endl;
}
}
int main (int argc, char* argv[]) {
string filename;
if (argc < 3) {
filename = "2000.in";
} else {
filename = argv[2];
}
Result result = read (filename);
vector< vector<int> > C = ijkalgorithm(result.A, result.B);
printMatrix(C);
return 0;
}
real 1m40.439s
user 1m38.642s
sys 0m0.280s
ikj-algorithm
Again, I've only switched line 61 and 62.
real 0m15.172s
user 0m14.877s
sys 0m0.248s
Library: Boost
If you want to compile these scripts, you might have to install the boost libraries first. On Ubuntu you can enter:
sudo apt-get install libboost-math*
#include <sstream>
#include <string>
#include <fstream>
#include <iostream>
#include <vector>
#include <boost/numeric/ublas/matrix.hpp>
#include <boost/numeric/ublas/io.hpp>
using namespace std;
struct Result {
boost::numeric::ublas::matrix<int> A;
boost::numeric::ublas::matrix<int> B;
};
int getMatrixSize(string filename) {
string line;
ifstream infile;
infile.open (filename.c_str());
getline(infile, line);
return count(line.begin(), line.end(), '\t') + 1;
}
void printMatrix(boost::numeric::ublas::matrix<int> matrix) {
for (unsigned int i=0; i < matrix.size1(); i++) {
for (unsigned int j=0; j < matrix.size2(); j++) {
cout << matrix(i, j);
if(j+1 != matrix.size2()) {
cout << "\t";
}
}
cout << endl;
}
}
Result read(string filename) {
Result ab;
string line;
ifstream infile;
infile.open (filename.c_str());
// get dimension
getline(infile, line);
int n = getMatrixSize(filename);
boost::numeric::ublas::matrix<int> A(n,n), B(n,n);
// process first line
istringstream iss(line);
int a, i = 0, j = 0;
while (iss >> a) {
A(i,j) = a;
j++;
}
i++;
while (getline(infile, line) && !line.empty()) {
istringstream iss(line);
j = 0;
while (iss >> a) {
A(i,j) = a;
j++;
}
i++;
}
i = 0;
while (getline(infile, line)) {
istringstream iss(line);
j = 0;
while (iss >> a) {
B(i,j) = a;
j++;
}
i++;
}
infile.close();
ab.A = A;
ab.B = B;
return ab;
}
int main (int argc, char* argv[]) {
string filename;
if (argc < 3) {
filename = "2000.in";
} else {
filename = argv[2];
}
Result result = read (filename);
boost::numeric::ublas::matrix<int> C;
C = boost::numeric::ublas::prod(result.A, result.B);
printMatrix(C);
return 0;
}
real 4m15.388s
user 4m10.272s
sys 0m0.588s
Library: Blitz
This is a great example of useless library. I've installed the library:
$ sudo apt-get install libblitz*
Then I wanted to use it. Well, I have no clue how I could exactly use it! See my StackOverflow Question: Is a documentation of Blitz++ matrices available?
Conclusion for C++

Again, it brings a performance boost if you know how your CPU works. I was very astonished, that the library Boost is slower (actually MUCH slower) than my simplest approach was.
Conclusion
If I want to create a working piece of code in a minimum amount of time, I will always take Python. It has been very easy to solve this task with the given restrictions. But C++ is amazing when speed is important.
It was astonishingly difficult to find working code examples for this task for Java and C++. I was searching for libraries and found some, but the search results were not satisfying.
See also
- Boost Matrix multiplication
- Rosetta Code: Matrix multiplication (Implementations in 63 programming languages!)
- Why is matrix multiplication faster with numpy than with ctypes in Python?
- Why is boosts matrix multiplication slower than mine?