Project Euler: Problem 35

The task in Problem 35 of Project Euler is:

The number, 197, is called a circular prime because all rotations of the digits: 197, 971, and 719, are themselves prime. There are thirteen such primes below 100: 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, and 97. How many circular primes are there below one million?

How to solve

If you have heard of the sieve of Eratosthenes, this one sounds quite easy:

  1. Find all primes below one million
  2. For each prime, do:
    1. Generate all rotations
    2. Check for every rotation if it is a prime
  3. Count the number of circular primes

The implementation

Sieve of Eratosthenes

The finds all primes below $n \in \mathbb{N}$. But you can make a lot of mistakes in the implementation.

First, this is the way the sieve of Eratosthenes works:

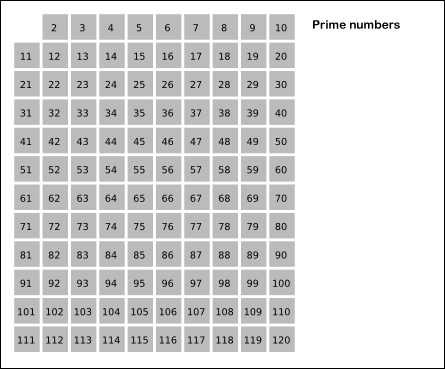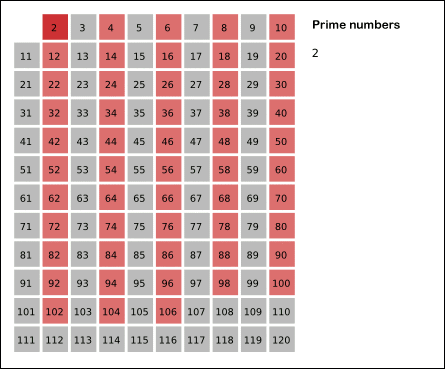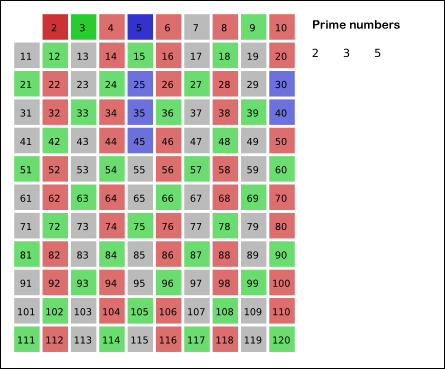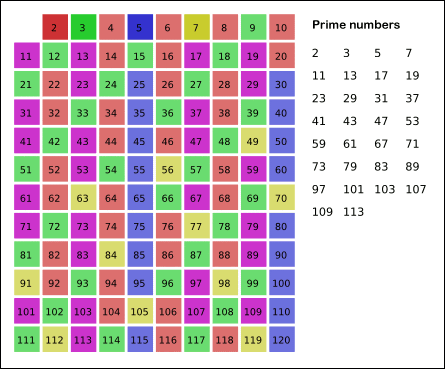
Sieve of Eratosthenes animation
Sieve of Eratosthenes: algorithm steps for primes below 121 (including optimization of starting from prime's square).
Source: Wikimedia

For example, this implementation is not good:

def getPrimesBelowN(n=1000000):
    """ Sieve of Eratosthenes """
    from math import ceil

    roundUp = lambda n, prime: int(ceil(float(n) / prime))

    primes = range(2, n)
    for currentPrime in primes:
        for multiplicant in range(2, roundUp(n, currentPrime)):
            noPrime = multiplicant * currentPrime
            if noPrime in primes:
                primes.remove(noPrime)
    return primes

Whats bad with this code? Well, just think about what it does: For every noPrime Python has to go through the whole list. I couldn't find how in is implemented, but I guess it is linear. So Python has to go through the whole list for in. Additionally, remove could also be expensive.

How could this get improved? Here is a better solution:

def getPrimesBelowN(n=1000000):
    """ Sieve of Eratosthenes """
    from math import ceil

    roundUp = lambda n, prime: int(ceil(float(n) / prime))

    primes = [True] * n
    primes[0] = False
    primes[1] = False
    primeList = []

    for currentPrime in range(2, n):
        if not primes[currentPrime]:
            continue
        primeList.append(currentPrime)
        for multiplicant in range(2, roundUp(n, currentPrime)):
            primes[multiplicant * currentPrime] = False
    return primeList

This solution does not need to search for noPrime, it simply jumps there in the list.

A generator version of the sieve of Erasthostenes can be found on code.activestate.com.

isCircularPrime

Rotation the digits of a number is the same as cutting the number into two pieces and switching the position of the pieces:

def isCircularPrime(primes, number):
    number = str(number)
    for i in range(0, len(number)):
        rotatedNumber = number[i : len(number)] + number[0:i]
        if int(rotatedNumber) not in primes:
            return False
    return True

Here is the same problem as above, in the sieving algorithm: Searching through the list takes much more time than jumping to a position in the list. So this one is better:

def isCircularPrime(primes, number):
    number = str(number)
    for i in range(0, len(number)):
        rotatedNumber = number[i : len(number)] + number[0:i]
        if not primes[int(rotatedNumber)]:
            return False
    return True

Some more speedups Every prime that contains one of the digits 0, 2, 4, 6 or 8 can't be a circular prime, because one rotation exist where that digit is at the end. This rotation would be divisible by 2 and thus not be a prime (except for 2, of course). You can use the same thought for the digit 5. So you can skip those digits

The final snippet

#!/usr/bin/env python
# -*- coding: utf-8 -*-


def getPrimesBelowN(n=1000000):
    """Get all primes below n with the sieve of Eratosthenes.
    @return: a list 0..n with boolean values that indicate if
             i in 0..n is a prime.
    """
    from math import ceil

    primes = [True] * n
    primes[0] = False
    primes[1] = False
    primeList = []
    roundUp = lambda n, prime: int(ceil(float(n) / prime))
    for currentPrime in range(2, n):
        if not primes[currentPrime]:
            continue
        primeList.append(currentPrime)
        for multiplicant in range(2, roundUp(n, currentPrime)):
            primes[multiplicant * currentPrime] = False
    return primes


def isCircularPrime(primes, number):
    """Check if number is a circular prime.

    Keyword arguments:
    primes -- a list from 0..n with boolean values that indicate if
              i in 0..n is a prime
    number -- the integer you want to check
    """
    number = str(number)
    for i in range(0, len(number)):
        rotatedNumber = number[i : len(number)] + number[0:i]
        if not primes[int(rotatedNumber)]:
            return False
    return True


if __name__ == "__main__":
    print("Start sieving.")
    primes = getPrimesBelowN(1000000)
    print("End sieving.")
    numberOfPrimes = 2
    print(2)  # I print them now, because I want to skip all primes
    print(5)  # that contain one of those digits: 0,2,4,5,6,8
    for prime, isPrime in enumerate(primes):
        if (
            (not isPrime)
            or ("2" in str(prime))
            or ("4" in str(prime))
            or ("6" in str(prime))
            or ("8" in str(prime))
            or ("0" in str(prime))
            or ("5" in str(prime))
        ):
            continue
        if isCircularPrime(primes, prime):
            print(prime)
            numberOfPrimes += 1

    print("Number of circular primes: %i" % numberOfPrimes)
It takes about 1.096 seconds (in comparison: having the version of isCircularPrime that searches through the list of primes took over 5 minutes!)

Published


by

Category

Code

Tags

Contact