I recently became interested in recommender systems. You know, the thing on Amazon that tells you which products you might be interested in. Or the stuff on Spotify that gives you a song you might like. On YouTube the next videos shown. On StumbleUpon, your next stumble. On a news page, another article.

Conceptual Approaches

There are three basic approaches:

• Product Similarity: You watched Saw I, Saw II and Saw III. All of them are similar to Saw IV.
• User similarity: Users that liked Saw I, Saw II and Saw III usually also liked Saw IV.
• Basket analysis: You bought eggs and sugar, maybe you want to buy milk as well.

Recommender systems based on product similarity are also called "content-based recommender systems". The New York Times article recommendation is an example for that.

Recommander systems based on user similarity are also called "collaborative filtering". movielens.org is an example for that.

Pandora is an example for content-based recommendation + collaborative filtering.

Basic Content-based Recommendations

Levenshteins edit distance applied on the product name is probably the simplest approach that has a mimimal chance of some reasonable results.

The next level in complexity are rules:

• Movies by a director you liked
• Movies with a actor you liked
• Count "links" (actors, directors, producers, ...) and rank by most links

One more level of complexity is using clustering algorithms. One way is to make a product to a vector and use a similarity measure (e.g. cosine similarity). If you have natural laguage descriptions you can use tf-idf features and then use a similarity measure. You would then recommend the most similar products.

Cosine-Similarity

Let $x$ and $y$ be items. Their cosine similarity is defined as $$f(x, y) := \frac{\sum_i x_i y_i}{\sqrt{\sum_i x_i^2} \sqrt{\sum_i y_i^2}}$$

Centered Cosine Similarity

Subtract the mean value from all elements. If you have null values, don't change anything there. Then apply the cosine similarity.

Jaccard Similarity

Let $x$ and $y$ be items and $r_x, r_y$ be their attributes. Their jaccard similarity is defined as $$f(x, y) := \frac{|r_x \cap r_y|}{|r_x \cup r_y|}$$

Minkowski Distance

$$f(x, y) := \left ( \sum_{i=1}^n {|x_i - y_i|}^p \right )^{1/p}$$

Mahalanobis distance

The Mahalanobis distance of an observation $\backslash vec\{x\}\; =\; (\; x\_1,\; x\_2,\; x\_3,\; \backslash dots,\; x\_N\; )^T$ from a set of observations with mean $\vec{\mu} = ( \mu_1, \mu_2, \mu_3, \dots , \mu_N )^T$ and covariance matrix $S$ is defined as: $$D_M(\vec{x}) = \sqrt{(\vec{x} - \vec{\mu})^T S^{-1} (\vec{x}-\vec{\mu})}$$

User-Based Collaborative Filtering

Users can have different scales on which they rate stuff:

• Binary: Like / Dislike (and "not seen")
• Ternary: Like / Neutral / Dislike (and "not seen")
• 5 Stars
• 100 points

So you want to find the utility function \(u: C \times I \rightarrow R\) where \(C\) is the set of customers, \(I\) is the set of items and \(R\) is the ordered set of ratings. By a simple transformation you can make it \(R = [0, 1]\).

The utility function \(u\) can be fully defined by a user-item rating matrix. Most elements of the matrix are not known, though.

Based on the user-item rating matrix \(R\) you build up a user-user similarity matrix.

You look up similar users, generate candidates for recommendation, score and filter candidates (items the user already knows).

See also: Collaborative Filtering

In some sense, bestellsers are a special case of collaborative filtering: Simply recommending what got sold most.

Adjusted Cosine

$$f(x, y) := \frac{\sum_i (x_i -\bar{x}) (y_i - \bar{y})}{\sqrt{\sum_i (x_i - \bar{x})^2} \sqrt{\sum_i (y_i - \bar{y})^2}}$$ Applicable mostly to get a similar user based on ratings. The idea is that different people have different baselines from which they operate, e.g. in a 5 star rating you could always give 5 stars if nothing is wrong. Or always 3 stars and if there is something really good, give more.

item-based pearson similarity

$$f(x, y) := \frac{\sum_i (x_i - \bar{j})(y_i - \bar{j})}{\sqrt{\sum_i (x_i - \bar{j})^2} \sqrt{\sum_i (y_i - \bar{j})^2}}$$

Spearman rank correlation

Pearson similarity based on ranks (position in the recommendation), not ratings. Usually not use in practice.

Mean Squared Difference Similarity

$$MSD(x, y) := \frac{\sum_{i \in I_{x, y}} (x_i - y_i)^2}{|I_{x, y}|}$$ and the similarity: $$MSDsim(x, y) := \frac{1}{MSD(x, y) + 1}$$

Jaccard Similarity

$$\frac{A \cap B}{A \cup B}$$

Basic Basket Analysis

See Association Rule Mining

More Collaborative Filtering

There are many Collaborative filtering (CF) approaches

Item-based collaborative filtering

"users who liked what you liked, also like..."

1. Build an item-item matrix determining relationships between pairs of items
2. Infer the tastes of the current user by examining the matrix and matching that user's data

Slope One is an example

Matrix Factorization

Factorize the rating matrix $R$ into a user-embedding matrix $U$ and an item embedding matrix $V$ such that $R = U \times \Sigma \times V$.

User-based collaborative filtering

1. Look for users who share the same rating patterns with the active user (the user whom the prediction is for).
2. Use the ratings from those like-minded users found in step 1 to calculate a prediction for the active user

k-NN is one example.

One line of work goes in the direction of matrix factorization with alternating least squares (ALS).[^5,^6] They have a training algorithm with has a time complexity of \(\mathcal{O}(MNK^2)\) for one iteration, where \(M\) is the number of users, \(N\) is the number of items and \(K\) is the dimension of the latent space.

Evaluation

There are two conceptually very different ways to think about recommender systems⁴:

• Matrix Completion: You have a matrix of user-item ratings. This matrix has many NULL values. You want to fill them.
• Ranking: Recommend the top-k items for a given user.

Matrix Completion

One way to evaluate if recommendation systems work is by the typical train-test split.

Possible Metrics, where \(y\) is the real value and \(p(x)\) is the predicted value:

Mean Absolute Error (MAE)

$\frac{1}{n} \sum_{i=1}^n |y_i - p(x_i)| \in [0, 1]$, where lower is better

Root Mean Square Error (RMSE)

$\sqrt{\frac{1}{n} \sum_{i=1}^n {(y_i - p(x_i))}^2} \in [0, \infty)$, where lower is better

Ranking

The problem with those two ways is that low-rated items don't matter much. If 95% of the users look at \(n\) items, then you want the Top-\(n\) recommendations to be (1) more relevant than the rest for the user and (2) the order of the top-\(n\) elements to be correct.

Metrics for top-n recommenders:

Precision@k

$\frac{\text{recommended items @k that are relevant}}{k}$. This gives you the portion of items that are relevant to your user.

Recall@k

$\frac{\text{recommended items @k that are relevant}}{total relevant items}$. If precision is high and recall is low, it might indicate that $k$ is just very small. If recall is high and precision is low it might show that not so many items are relevant in comparison to the choice of $k$.

Average Precision@k

TODO

Hit Rate

Number of hits in your $n$ recommendations, divided by the number of users

Average Reciprocal Hit Rank (ARHR)

$\frac{1}{|Users| \cdot \sum_{i=1}^n \frac{1}{rank_i}}$

Cumulative Hit Rate (cHR)

Throw away low-ranking stuff (hence you need a threshold)

Other

Other quality indicators for a recommendation system

Diversity

How broad is the variety of items recommended to people?

Novelty

How many new/unfamiliar things do get recommended to a user? The higher the novelty, the more likely the user will discover something new. If it is too high, the user doesn't trust the recommendation anymore.

Churn

How often do recommendations for a user change?

Responsiveness

How quickly are recommendations adjusted?

User Feedback

Another way to evaluate is to ask the user:

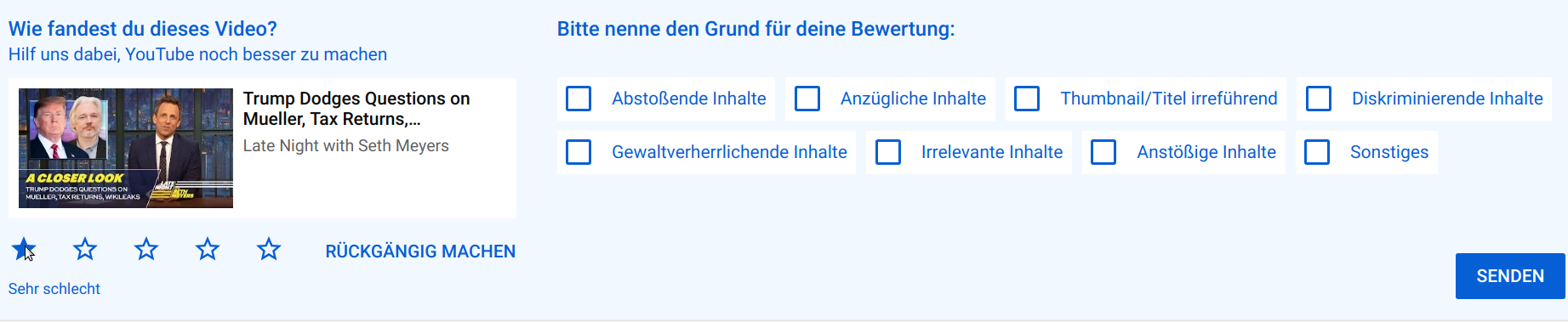
Typical Problems

Cold-Start Problem

The cold-start problem is central and only fixable by content-based recommendation. If there is a new product, not a single user has rated it. It is not possible by collaborative filtering to recommend it.

Sparsity

You have so many items, that two users have no item in common and two items usually don't have properties in common.

Wrong Recommendation Mode

• You have bought the DVD "Lord of the Rings" and get the Blue Ray recommended.
• You have liked the normal version of a song and you get the techno/rap/christmas version recommended

The Bubble

• You will never be recommended a movie where you didn't like the genre before.

Surrogate-Problem

Ultimatively, we want to maximize user engagement. In order to achieve this, we define a surrogate (e.g. accuracy of predicting user ratings).

The problem is that the choice of the surrogate matters a lot. A different surrogate might have way bigger impact on our real goal than an improvement in achieving the surrogate goal.

Vocabulary

Top-N Recommendation

Recommend N items

mise en scène

The idea in content-based filtering for movies to extract properties directly from the movie itself. It includes: Average shot length, color variance, mean motion average across all the frames, lightning, number of shots

Matrix Factorization

Matrix Factorization is factorization in the same way as with natural numbers: Take a matrix \(R\) and factorize it in \(U\) and \(V\) such that \(R = U \cdot V\). If the complete matrix \(R\) is given, \(R\) can be factorized with Singular Value Decomposition (SVD) or Probabilistic Latent Semantic Analysis (PLSA).

Matrix Factorization is also one way to do collaborative filtering. It was done for the Netflix prize and is described in ³. A neat short description is in SurpriseLib.

Input: The ratings of \(n\) users for \(m\) movies in a matrix \(R \in \mathbb{R}^{n \times m}\).

Algorithm: Singular value decomposition (SVD) takes \(R\) and gives three matrices \(U \in \mathbb{R}^{n \times r}\), a descendingly sorted diagonal matrix \(\Sigma \in \mathbb{R}^{r \times r}\) and \(V \in \mathbb{R}^{r \times m}\) such that \(R = U \cdot \Sigma \cdot V\).

The rows in \(U\) represent the users. It's called the "latent space". Latent is math slang for "hidden" (see latent variable). This means we have a reasonable way to represent users.

The rows in \(V\) represent the movies in the latent space.

You crop at some point of \(\Sigma\) to the first \(k\) singular features (with \(k < r\)).

The problem is that many values of \(R\) are missing. Simon Funk found a solution to that problem. Instead of imputing the values (filling the matrix), he re-formulated the problem to

This is a minimization problem that can be solved by gradient descent. As you only consider values \(p_{ij}\) that are not zero, you don't have to invent the remainding ones.

Code

• Github: recommender-system
• benfred/implicit

Datasets

• MovieLens 100K Dataset
• Last.fm dataset / Last.fm 360k / Last.fm 1k

Other Resources

• Meaning of latent features?
• Simon Funk: Netflix Update: Try This at Home
• Houtao Deng: Recommender Systems in Practice, 2019.
• Victor: ALS Implicit Collaborative Filtering, 2017 - explains ⁶ neatly.
• Implicit
  • Ben Frederickson: Faster Implicit Matrix Factorization, 12.12.2016.
  • Ben Frederickson: Finding Similar Music using Matrix Factorization, 02.10.2017.

Not read so far:

• Leskovec, Rajaraman, Ullman: Collaborative Filtering. Lecture 43 of "Mininig of Massive Datasets". Stanford University.
• Maher Malaeb: The easy guide for building python collaborative filtering recommendation system, 2017.
• surprise docs
• surprise gist
• Houtao Deng: Recommender Systems in Practice, 2013
• Kaggle: Tutorials Recommendation System, 2019.

Papers