The usual matrix multiplication of two $n \times n$ matrices has a time-complexity of $\mathcal{O}(n^3)$. This means, if $n$ doubles, the time for the computation increases by a factor of 8. But you don't have to use that much resources. The Strassen algorithm has a time complexity of $\mathcal O(n^{log_2(7)+o(1)}) \approx \cal O(n^{2.807})$. The idea is similar to the Karatsuba algorithm for simple multiplication. Basically, you make a tradeof: Instead of one multiplication, you use many additions. As additions are - at least for humans - easier, you might rather like to use many additions. Lets see how the Strassen algortihms execution time compares to the other execution times in Part I. As last time, I'll multiply two $2000 \times 2000$ matrices that have to be read from a file. Everything - reading, calculation and writing the result - counts to the execution time.
The implementations
As last time, I've added the scripts to a GIT repository, so feel free to test it on your machine. I will use the I am also happy if you post some of your solutions with running times ☺ If you know other languages, you could create a script for these. I focus on Python, Java and C++.
I have implemented only the Strassen algorithm for this post. Please take a look at Wikipedia for a detailed explanation how this algorithm works. The important idea of the algorithm is that you break both matrices into four $\frac{n}{2} \times \frac{n}{2}$ matrices and multiply them in a clever way. Note that you can also use the Strassen algorithm recursively for those $\frac{n}{2} \times \frac{n}{2}$ matrices. You can do this until you have $1 \times 1$ matrices which are simple numbers. But it does make sense to stop this recursion and use the ikj-algorithm as soon as the matrices are small enough. But what exactly is "small enough"? I'll test that. The size when you use the ikj-algorithm is called LEAF_SIZE in my scripts. Note that only leaf sizes of multiples of two matter as the size of the (sub-)matrices that get passed to strassenR are multiples of two.
If you post a solution, please consider these restrictions:
- Input:
- The input file should get passed with the parameter
-i, e.g.:python -i bigMatrix.inorjava Shell -i bigMatrix.in - The leaf-size should get passed with
-l, e.g.:python -i bigMatrix.in -l 32
- The input file should get passed with the parameter
- The standard value for the command line parameter -i should be "bigMatrix.in"
- The user should not have to give the size of the matrix!
- The two square-matrices that should get multiplied are ...
- ... read from a text-file.
- ... represented like this:
- Every line of one matrix is one line in the text-file.
- Newlines are only "\n".
- Every number is separated by "\t".
- The both matrices are separated by one newline.
- Output: The result has to get printed to standard output.
- The result has to be formatted like the input (tabs for separation of number, \n for marks a new line)
Tests and Setting
Tests and setting are the same as in the first part.
Python
I’ve used Python 2.6.5.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from optparse import OptionParser
from math import ceil, log
def read(filename):
lines = open(filename, "r").read().splitlines()
A = []
B = []
matrix = A
for line in lines:
if line != "":
matrix.append(map(int, line.split("\t")))
else:
matrix = B
return A, B
def printMatrix(matrix):
for line in matrix:
print("\t".join(map(str, line)))
def ikjMatrixProduct(A, B):
n = len(A)
C = [[0 for i in range(n)] for j in range(n)]
for i in range(n):
for k in range(n):
for j in range(n):
C[i][j] += A[i][k] * B[k][j]
return C
def add(A, B):
n = len(A)
C = [[0 for j in range(0, n)] for i in range(0, n)]
for i in range(0, n):
for j in range(0, n):
C[i][j] = A[i][j] + B[i][j]
return C
def subtract(A, B):
n = len(A)
C = [[0 for j in range(0, n)] for i in range(0, n)]
for i in range(0, n):
for j in range(0, n):
C[i][j] = A[i][j] - B[i][j]
return C
def strassenR(A, B):
"""
Implementation of the strassen algorithm.
"""
n = len(A)
if n <= LEAF_SIZE:
return ikjMatrixProduct(A, B)
else:
# initializing the new sub-matrices
newSize = n / 2
a11 = [[0 for j in range(0, newSize)] for i in range(0, newSize)]
a12 = [[0 for j in range(0, newSize)] for i in range(0, newSize)]
a21 = [[0 for j in range(0, newSize)] for i in range(0, newSize)]
a22 = [[0 for j in range(0, newSize)] for i in range(0, newSize)]
b11 = [[0 for j in range(0, newSize)] for i in range(0, newSize)]
b12 = [[0 for j in range(0, newSize)] for i in range(0, newSize)]
b21 = [[0 for j in range(0, newSize)] for i in range(0, newSize)]
b22 = [[0 for j in range(0, newSize)] for i in range(0, newSize)]
aResult = [[0 for j in range(0, newSize)] for i in range(0, newSize)]
bResult = [[0 for j in range(0, newSize)] for i in range(0, newSize)]
# dividing the matrices in 4 sub-matrices:
for i in range(0, newSize):
for j in range(0, newSize):
a11[i][j] = A[i][j] # top left
a12[i][j] = A[i][j + newSize] # top right
a21[i][j] = A[i + newSize][j] # bottom left
a22[i][j] = A[i + newSize][j + newSize] # bottom right
b11[i][j] = B[i][j] # top left
b12[i][j] = B[i][j + newSize] # top right
b21[i][j] = B[i + newSize][j] # bottom left
b22[i][j] = B[i + newSize][j + newSize] # bottom right
# Calculating p1 to p7:
aResult = add(a11, a22)
bResult = add(b11, b22)
p1 = strassenR(aResult, bResult) # p1 = (a11+a22) * (b11+b22)
aResult = add(a21, a22) # a21 + a22
p2 = strassenR(aResult, b11) # p2 = (a21+a22) * (b11)
bResult = subtract(b12, b22) # b12 - b22
p3 = strassenR(a11, bResult) # p3 = (a11) * (b12 - b22)
bResult = subtract(b21, b11) # b21 - b11
p4 = strassenR(a22, bResult) # p4 = (a22) * (b21 - b11)
aResult = add(a11, a12) # a11 + a12
p5 = strassenR(aResult, b22) # p5 = (a11+a12) * (b22)
aResult = subtract(a21, a11) # a21 - a11
bResult = add(b11, b12) # b11 + b12
p6 = strassenR(aResult, bResult) # p6 = (a21-a11) * (b11+b12)
aResult = subtract(a12, a22) # a12 - a22
bResult = add(b21, b22) # b21 + b22
p7 = strassenR(aResult, bResult) # p7 = (a12-a22) * (b21+b22)
# calculating c21, c21, c11 e c22:
c12 = add(p3, p5) # c12 = p3 + p5
c21 = add(p2, p4) # c21 = p2 + p4
aResult = add(p1, p4) # p1 + p4
bResult = add(aResult, p7) # p1 + p4 + p7
c11 = subtract(bResult, p5) # c11 = p1 + p4 - p5 + p7
aResult = add(p1, p3) # p1 + p3
bResult = add(aResult, p6) # p1 + p3 + p6
c22 = subtract(bResult, p2) # c22 = p1 + p3 - p2 + p6
# Grouping the results obtained in a single matrix:
C = [[0 for j in range(0, n)] for i in range(0, n)]
for i in range(0, newSize):
for j in range(0, newSize):
C[i][j] = c11[i][j]
C[i][j + newSize] = c12[i][j]
C[i + newSize][j] = c21[i][j]
C[i + newSize][j + newSize] = c22[i][j]
return C
def strassen(A, B):
assert type(A) == list and type(B) == list
assert len(A) == len(A[0]) == len(B) == len(B[0])
# Make the matrices bigger so that you can apply the strassen
# algorithm recursively without having to deal with odd
# matrix sizes
nextPowerOfTwo = lambda n: 2 ** int(ceil(log(n, 2)))
n = len(A)
m = nextPowerOfTwo(n)
APrep = [[0 for i in range(m)] for j in range(m)]
BPrep = [[0 for i in range(m)] for j in range(m)]
for i in range(n):
for j in range(n):
APrep[i][j] = A[i][j]
BPrep[i][j] = B[i][j]
CPrep = strassenR(APrep, BPrep)
C = [[0 for i in range(n)] for j in range(n)]
for i in range(n):
for j in range(n):
C[i][j] = CPrep[i][j]
return C
if __name__ == "__main__":
parser = OptionParser()
parser.add_option(
"-i",
dest="filename",
default="2000.in",
help="input file with two matrices",
metavar="FILE",
)
parser.add_option(
"-l",
dest="LEAF_SIZE",
default="8",
help="when do you start using ikj",
metavar="LEAF_SIZE",
)
(options, args) = parser.parse_args()
LEAF_SIZE = options.LEAF_SIZE
A, B = read(options.filename)
C = strassen(A, B)
printMatrix(C)
The execution-times were the same as with the ikj-algorithm, no matter what the leaf size was:
ikj-algorithm 44m13.458s
LEAF_SIZE Time
2 47m45.983s
8 47m41.311s
16 48m5.472s
32 48m5.624s
64 47m55.076s
Java
The Java-code is a little bit long and has three classes. I'll only past the important methods. If you're interested in a full, working example, please look at GitHub.
public static int[][] ikjAlgorithm(int[][] A, int[][] B) {
int n = A.length;
// initialise C
int[][] C = new int[n][n];
for (int i = 0; i < n; i++) {
for (int k = 0; k < n; k++) {
for (int j = 0; j < n; j++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
return C;
}
private static int[][] add(int[][] A, int[][] B) {
int n = A.length;
int[][] C = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
C[i][j] = A[i][j] + B[i][j];
}
}
return C;
}
private static int[][] subtract(int[][] A, int[][] B) {
int n = A.length;
int[][] C = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
C[i][j] = A[i][j] - B[i][j];
}
}
return C;
}
private static int nextPowerOfTwo(int n) {
int log2 = (int) Math.ceil(Math.log(n) / Math.log(2));
return (int) Math.pow(2, log2);
}
public static int[][] strassen(ArrayList<ArrayList<Integer>> A,
ArrayList<ArrayList<Integer>> B) {
// Make the matrices bigger so that you can apply the strassen
// algorithm recursively without having to deal with odd
// matrix sizes
int n = A.size();
int m = nextPowerOfTwo(n);
int[][] APrep = new int[m][m];
int[][] BPrep = new int[m][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
APrep[i][j] = A.get(i).get(j);
BPrep[i][j] = B.get(i).get(j);
}
}
int[][] CPrep = strassenR(APrep, BPrep);
int[][] C = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
C[i][j] = CPrep[i][j];
}
}
return C;
}
private static int[][] strassenR(int[][] A, int[][] B) {
int n = A.length;
if (n <= LEAF_SIZE) {
return ikjAlgorithm(A, B);
} else {
// initializing the new sub-matrices
int newSize = n / 2;
int[][] a11 = new int[newSize][newSize];
int[][] a12 = new int[newSize][newSize];
int[][] a21 = new int[newSize][newSize];
int[][] a22 = new int[newSize][newSize];
int[][] b11 = new int[newSize][newSize];
int[][] b12 = new int[newSize][newSize];
int[][] b21 = new int[newSize][newSize];
int[][] b22 = new int[newSize][newSize];
int[][] aResult = new int[newSize][newSize];
int[][] bResult = new int[newSize][newSize];
// dividing the matrices in 4 sub-matrices:
for (int i = 0; i < newSize; i++) {
for (int j = 0; j < newSize; j++) {
a11[i][j] = A[i][j]; // top left
a12[i][j] = A[i][j + newSize]; // top right
a21[i][j] = A[i + newSize][j]; // bottom left
a22[i][j] = A[i + newSize][j + newSize]; // bottom right
b11[i][j] = B[i][j]; // top left
b12[i][j] = B[i][j + newSize]; // top right
b21[i][j] = B[i + newSize][j]; // bottom left
b22[i][j] = B[i + newSize][j + newSize]; // bottom right
}
}
// Calculating p1 to p7:
aResult = add(a11, a22);
bResult = add(b11, b22);
int[][] p1 = strassenR(aResult, bResult);
// p1 = (a11+a22) * (b11+b22)
aResult = add(a21, a22); // a21 + a22
int[][] p2 = strassenR(aResult, b11); // p2 = (a21+a22) * (b11)
bResult = subtract(b12, b22); // b12 - b22
int[][] p3 = strassenR(a11, bResult);
// p3 = (a11) * (b12 - b22)
bResult = subtract(b21, b11); // b21 - b11
int[][] p4 = strassenR(a22, bResult);
// p4 = (a22) * (b21 - b11)
aResult = add(a11, a12); // a11 + a12
int[][] p5 = strassenR(aResult, b22);
// p5 = (a11+a12) * (b22)
aResult = subtract(a21, a11); // a21 - a11
bResult = add(b11, b12); // b11 + b12
int[][] p6 = strassenR(aResult, bResult);
// p6 = (a21-a11) * (b11+b12)
aResult = subtract(a12, a22); // a12 - a22
bResult = add(b21, b22); // b21 + b22
int[][] p7 = strassenR(aResult, bResult);
// p7 = (a12-a22) * (b21+b22)
// calculating c21, c21, c11 e c22:
int[][] c12 = add(p3, p5); // c12 = p3 + p5
int[][] c21 = add(p2, p4); // c21 = p2 + p4
aResult = add(p1, p4); // p1 + p4
bResult = add(aResult, p7); // p1 + p4 + p7
int[][] c11 = subtract(bResult, p5);
// c11 = p1 + p4 - p5 + p7
aResult = add(p1, p3); // p1 + p3
bResult = add(aResult, p6); // p1 + p3 + p6
int[][] c22 = subtract(bResult, p2);
// c22 = p1 + p3 - p2 + p6
// Grouping the results obtained in a single matrix:
int[][] C = new int[n][n];
for (int i = 0; i < newSize; i++) {
for (int j = 0; j < newSize; j++) {
C[i][j] = c11[i][j];
C[i][j + newSize] = c12[i][j];
C[i + newSize][j] = c21[i][j];
C[i + newSize][j + newSize] = c22[i][j];
}
}
return C;
}
}
Here are the results for different leaf-sizes:
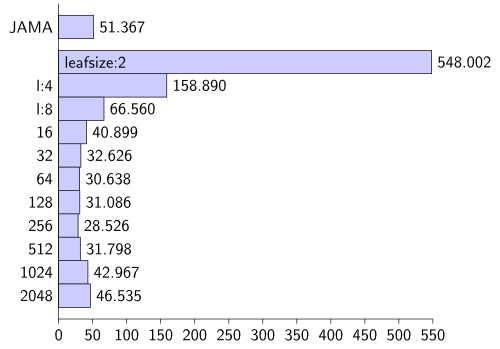
C++
#include <sstream>
#include <string>
#include <fstream>
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
// Set LEAF_SIZE to 1 if you want to the pure strassen algorithm
// otherwise, the ikj-algorithm will be applied when the split
// matrices are as small as LEAF_SIZE x LEAF_SIZE
int leafsize;
using namespace std;
/*
* Implementation of the strassen algorithm, similar to
* http://en.wikipedia.org/w/index.php?title=Strassen_algorithm&oldid=498910018#Source_code_of_the_Strassen_algorithm_in_C_language
*/
void strassen(vector< vector<int> > &A,
vector< vector<int> > &B,
vector< vector<int> > &C, unsigned int tam);
unsigned int nextPowerOfTwo(int n);
void strassenR(vector< vector<int> > &A,
vector< vector<int> > &B,
vector< vector<int> > &C,
int tam);
void sum(vector< vector<int> > &A,
vector< vector<int> > &B,
vector< vector<int> > &C, int tam);
void subtract(vector< vector<int> > &A,
vector< vector<int> > &B,
vector< vector<int> > &C, int tam);
void printMatrix(vector< vector<int> > matrix, int n);
void read(string filename, vector< vector<int> > &A, vector< vector<int> > &B);
void ikjalgorithm(vector< vector<int> > A,
vector< vector<int> > B,
vector< vector<int> > &C, int n) {
for (int i = 0; i < n; i++) {
for (int k = 0; k < n; k++) {
for (int j = 0; j < n; j++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
}
void strassenR(vector< vector<int> > &A,
vector< vector<int> > &B,
vector< vector<int> > &C, int tam) {
if (tam <= leafsize) {
ikjalgorithm(A, B, C, tam);
return;
}
// other cases are treated here:
else {
int newTam = tam/2;
vector<int> inner (newTam);
vector< vector<int> >
a11(newTam,inner), a12(newTam,inner), a21(newTam,inner), a22(newTam,inner),
b11(newTam,inner), b12(newTam,inner), b21(newTam,inner), b22(newTam,inner),
c11(newTam,inner), c12(newTam,inner), c21(newTam,inner), c22(newTam,inner),
p1(newTam,inner), p2(newTam,inner), p3(newTam,inner), p4(newTam,inner),
p5(newTam,inner), p6(newTam,inner), p7(newTam,inner),
aResult(newTam,inner), bResult(newTam,inner);
int i, j;
//dividing the matrices in 4 sub-matrices:
for (i = 0; i < newTam; i++) {
for (j = 0; j < newTam; j++) {
a11[i][j] = A[i][j];
a12[i][j] = A[i][j + newTam];
a21[i][j] = A[i + newTam][j];
a22[i][j] = A[i + newTam][j + newTam];
b11[i][j] = B[i][j];
b12[i][j] = B[i][j + newTam];
b21[i][j] = B[i + newTam][j];
b22[i][j] = B[i + newTam][j + newTam];
}
}
// Calculating p1 to p7:
sum(a11, a22, aResult, newTam); // a11 + a22
sum(b11, b22, bResult, newTam); // b11 + b22
strassenR(aResult, bResult, p1, newTam); // p1 = (a11+a22) * (b11+b22)
sum(a21, a22, aResult, newTam); // a21 + a22
strassenR(aResult, b11, p2, newTam); // p2 = (a21+a22) * (b11)
subtract(b12, b22, bResult, newTam); // b12 - b22
strassenR(a11, bResult, p3, newTam); // p3 = (a11) * (b12 - b22)
subtract(b21, b11, bResult, newTam); // b21 - b11
strassenR(a22, bResult, p4, newTam); // p4 = (a22) * (b21 - b11)
sum(a11, a12, aResult, newTam); // a11 + a12
strassenR(aResult, b22, p5, newTam); // p5 = (a11+a12) * (b22)
subtract(a21, a11, aResult, newTam); // a21 - a11
sum(b11, b12, bResult, newTam); // b11 + b12
strassenR(aResult, bResult, p6, newTam); // p6 = (a21-a11) * (b11+b12)
subtract(a12, a22, aResult, newTam); // a12 - a22
sum(b21, b22, bResult, newTam); // b21 + b22
strassenR(aResult, bResult, p7, newTam); // p7 = (a12-a22) * (b21+b22)
// calculating c21, c21, c11 e c22:
sum(p3, p5, c12, newTam); // c12 = p3 + p5
sum(p2, p4, c21, newTam); // c21 = p2 + p4
sum(p1, p4, aResult, newTam); // p1 + p4
sum(aResult, p7, bResult, newTam); // p1 + p4 + p7
subtract(bResult, p5, c11, newTam); // c11 = p1 + p4 - p5 + p7
sum(p1, p3, aResult, newTam); // p1 + p3
sum(aResult, p6, bResult, newTam); // p1 + p3 + p6
subtract(bResult, p2, c22, newTam); // c22 = p1 + p3 - p2 + p6
// Grouping the results obtained in a single matrix:
for (i = 0; i < newTam ; i++) {
for (j = 0 ; j < newTam ; j++) {
C[i][j] = c11[i][j];
C[i][j + newTam] = c12[i][j];
C[i + newTam][j] = c21[i][j];
C[i + newTam][j + newTam] = c22[i][j];
}
}
}
}
unsigned int nextPowerOfTwo(int n) {
return pow(2, int(ceil(log2(n))));
}
void strassen(vector< vector<int> > &A,
vector< vector<int> > &B,
vector< vector<int> > &C, unsigned int n) {
//unsigned int n = tam;
unsigned int m = nextPowerOfTwo(n);
vector<int> inner(m);
vector< vector<int> > APrep(m, inner), BPrep(m, inner), CPrep(m, inner);
for(unsigned int i=0; i<n; i++) {
for (unsigned int j=0; j<n; j++) {
APrep[i][j] = A[i][j];
BPrep[i][j] = B[i][j];
}
}
strassenR(APrep, BPrep, CPrep, m);
for(unsigned int i=0; i<n; i++) {
for (unsigned int j=0; j<n; j++) {
C[i][j] = CPrep[i][j];
}
}
}
void sum(vector< vector<int> > &A,
vector< vector<int> > &B,
vector< vector<int> > &C, int tam) {
int i, j;
for (i = 0; i < tam; i++) {
for (j = 0; j < tam; j++) {
C[i][j] = A[i][j] + B[i][j];
}
}
}
void subtract(vector< vector<int> > &A,
vector< vector<int> > &B,
vector< vector<int> > &C, int tam) {
int i, j;
for (i = 0; i < tam; i++) {
for (j = 0; j < tam; j++) {
C[i][j] = A[i][j] - B[i][j];
}
}
}
int getMatrixSize(string filename) {
string line;
ifstream infile;
infile.open (filename.c_str());
getline(infile, line);
return count(line.begin(), line.end(), '\t') + 1;
}
void read(string filename, vector< vector<int> > &A, vector< vector<int> > &B) {
string line;
FILE* matrixfile = freopen(filename.c_str(), "r", stdin);
if (matrixfile == 0) {
cerr << "Could not read file " << filename << endl;
return;
}
int i = 0, j, a;
while (getline(cin, line) && !line.empty()) {
istringstream iss(line);
j = 0;
while (iss >> a) {
A[i][j] = a;
j++;
}
i++;
}
i = 0;
while (getline(cin, line)) {
istringstream iss(line);
j = 0;
while (iss >> a) {
B[i][j] = a;
j++;
}
i++;
}
fclose (matrixfile);
}
void printMatrix(vector< vector<int> > matrix, int n) {
for (int i=0; i < n; i++) {
for (int j=0; j < n; j++) {
if (j != 0) {
cout << "\t";
}
cout << matrix[i][j];
}
cout << endl;
}
}
int main (int argc, char* argv[]) {
string filename;
if (argc < 3) {
filename = "2000.in";
} else {
filename = argv[2];
}
if (argc < 5) {
leafsize = 16;
} else {
leafsize = atoi(argv[4]);
}
int n = getMatrixSize(filename);
vector<int> inner (n);
vector< vector<int> > A(n, inner), B(n, inner), C(n, inner);
read (filename, A, B);
strassen(A, B, C, n);
printMatrix(C, n);
return 0;
}
For C++, you get those user-times for the different leaf-sizes:

Conclusion
As always, C++ is the fastest solution.
I am a little bit surprised, that the LEAF_SIZE doesn't matter for Python. I think I have used some very slow operations that are much more important than any speed gains or losses due to LEAF_SIZE. I guess the list creation might be slow. Does anybody know a tool for performance analysis of Python programs? This tool should be able to track which pieces of code got executed most often any preferably visualize it.
For Java and C++, the Strassen algorithm had better execution times than the ikj-algorithm and it was also better than any library that I could find. The reasons why librarys perform worse than my implementation might be that pure integer matrices are rather rare. Usually you have double-matrices. Maybe you use different algorithms to keep rounding errors as small as possible (Can anybody provide more information to my speculations?)
Leafsizes from 64 to 256 seem to be the best solution.