The goal of this post is to show you some tools that allow you to visualize data. And I also want to analyze some basic characteristics of the Collatz sequence.
The Collatz sequences \((c^n_i)\) of a number \(n \in \mathbb{N}_{> 0}\) is defined like this:
So the sequence \((c^n_{i})\) is defined as:
You can define a directed graph \(G=(V, E)\) like this:
\(V = \mathbb{N}_{>0}, \;\;\; E = \{(n, f(n)) | n \in V\}\)
I will call this the Collatz graph.
Collatz conjecture
The Collatz conjecture was not (dis)proved by now. This is astonishing, as it was proposed in 1937 and I think it is very easy to understand.
We also don't know if the Collatz graph is connected. When it is not connected, it could be that one sequence \((c^n_i)\) goes to infinity or that there is another circle (\(4,2,1,4\) is a circle in the Collatz graph).
Small $n$
When you go through all possible Collatz sequences with \(n \in 1, \dots, 15\), this is what you get:
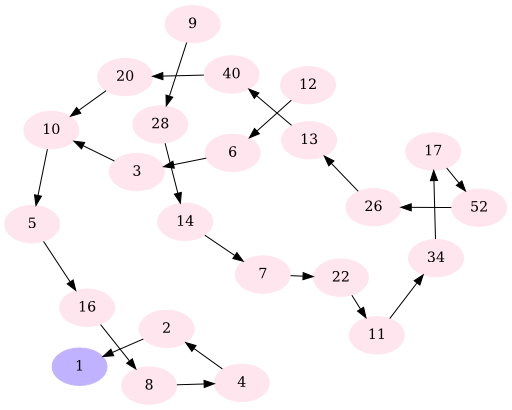
This image was created with the following Python script:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Based on: http://en.wikipedia.org/wiki/File:Collatz-graph-all-30-no27.svg
def f(n):
if n % 2 == 0:
return n / 2
else:
return 3 * n + 1
def writeDotfile(filename, limit, explored):
dotfile = file(filename, "w")
dotfile.write("digraph {\n")
dotfile.write('node[style=filled,color=".7 .3 1.0"];\n')
dotfile.write("1\n")
dotfile.write('node[style=filled,color=".95 .1 1"];\n')
# dotfile.write('size="15,8";\n')
for n in range(2, limit):
while n not in explored:
dotfile.write(str(n) + " -> ")
explored.add(n)
n = f(n)
dotfile.write(str(n) + ";\n")
dotfile.write("}\n")
def createPng(dotfile, base, program):
import os
command = program + " -Tsvg " + dotfile + " -o " + base + ".svg"
print("Execute command: %s" % command)
os.system(command)
command = "inkscape " + base + ".svg" + " -w 512 --export-png=" + base + ".png"
print("Execute command: %s" % command)
os.system(command)
if __name__ == "__main__":
import argparse
parser = argparse.ArgumentParser(description="Graph for small Collatz sequences")
parser.add_argument(
"-f",
"--file",
dest="filename",
default="collatz-graph.gv",
help="write dot-FILE",
metavar="FILE",
)
parser.add_argument(
"-p",
"--program",
dest="program",
help="dot, neato, twopi, circo, fdp, sfdp, osage",
metavar="PROGRAM",
default="dot",
)
parser.add_argument("-n", dest="limit", default=20, type=int, help="limit")
args = parser.parse_args()
writeDotfile(args.filename, args.limit, set([1]))
import os
createPng(args.filename, os.path.splitext(args.filename)[0], args.program)
called like this:
python small-numbers.py -n 15 -p fdp
$n=27$
\(n=27\) is an enourmously long sequence:
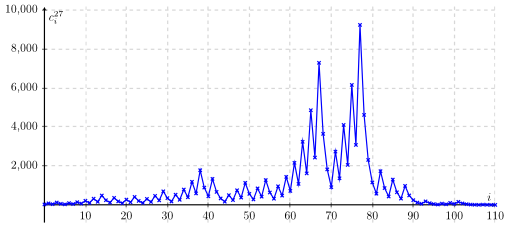
It was created with pgfplots:
\documentclass[varwidth=true, border=2pt]{standalone}
\usepackage[margin=2.5cm]{geometry} %layout
\usepackage{pgfplots}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
axis x line=middle,
axis y line=middle,
enlarge y limits=true,
scaled y ticks = false,
width=15cm, height=8cm, % size of the image
grid = major,
grid style={dashed, gray!30},
ylabel=$c^{27}_i$,
xlabel=$i$,
legend style={at={(0.1,-0.1)}, anchor=north}
]
\addplot[sharp plot, mark=x, blue] table [x=steps, y=n, col sep=comma] {../collatz27.csv};
\end{axis}
\end{tikzpicture}
\end{document}
How long are Collatz sequences?
I've been interested in the question how long Collatz sequences are. Of course, they will be longer when \(n\) is bigger. But how does the choice of \(n\) influence the number of steps it takes until you reach \(c^n_i = 1\)?
I've tested all Collatz sequences with \(n \leq 10,000,000\). This is the result:
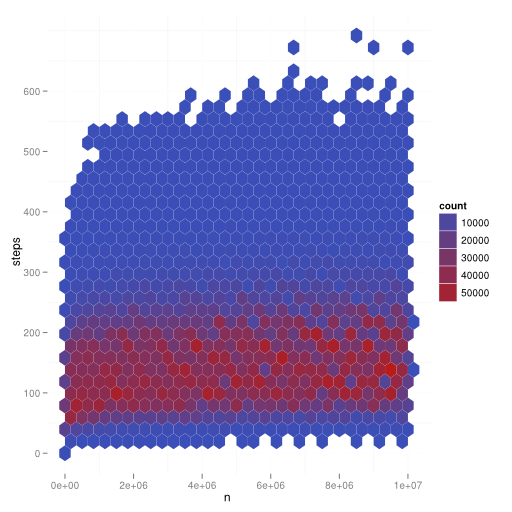
For every hexagon, you check how many datapoints \((n,steps)\) you have there. This leads to the count. As you can see, step numbers from 50-120 are very common, the rest is very uncommon. The number of steps increases very slow.
The data was created as a 116.9 MB csv file with this C++ code:
#include <iostream>
#include <string>
#include <map>
#include <vector>
#include <climits> // get maximum value of unsigned long long
#include <cstdlib> // exit
#define SURPRESS_OUTPUT true
#define SHOW_DICT_CREATION false
using namespace std;
struct element {
/** What is the next collatz number? */
unsigned long long next;
/** How many steps does it take until you reach 1? */
unsigned long long steps;
};
map<unsigned long long, struct element> collatz;
unsigned long long CRITICAL_VALUE = (ULLONG_MAX-1) / 3;
unsigned long long maxAddFromOneEntry = 0;
unsigned long long maxEntry = 0;
unsigned long long maxStepsToOne = 0;
unsigned long long saveULong = 0;
/** n >= 1 */
unsigned long long nextCollatz(unsigned long long n) {
if (n%2 == 0) {
return n/2;
} else {
if (n >= CRITICAL_VALUE) {
cerr << "Critical value is: " << CRITICAL_VALUE << endl;
cerr << "n is: " << n << endl;
cerr << "saveULong is: " << saveULong << endl;
exit(1);
}
return 3*n+1;
}
}
void insertCollatz(unsigned long long i){
if (collatz.find(i) == collatz.end()) {
if (SHOW_DICT_CREATION && !SURPRESS_OUTPUT) {
cout << i << " is not in collatz:" << endl;
}
// i is not in collatz
vector<unsigned long long> steps;
unsigned long long current = i;
unsigned long long next = nextCollatz(current);
while(collatz.find(current) == collatz.end()) {
steps.push_back(current);
current = next;
next = nextCollatz(current);
}
if (steps.size() > maxAddFromOneEntry) {
maxAddFromOneEntry = steps.size();
}
vector<unsigned long long>::reverse_iterator it;
for(it=steps.rbegin(); it != steps.rend(); it++){
struct element el;
el.next = current;
el.steps = collatz[current].steps + 1;
collatz[*it] = el;
if (el.steps > maxStepsToOne) {
maxStepsToOne = el.steps;
}
if (*it > maxEntry) {
maxEntry = *it;
}
current = *it;
if (SHOW_DICT_CREATION && !SURPRESS_OUTPUT) {
cout << "\tinserted " << *it << "->" << el.next << endl;
}
}
return;
} else if (SHOW_DICT_CREATION && !SURPRESS_OUTPUT) {
cout << i << " was already in collatz." << endl;
}
}
void printCollatz() {
for(map<unsigned long long, struct element>::iterator it=collatz.begin();
it!=collatz.end(); ++it) {
unsigned long long next = (*it).first;
while(next != 1) {
cout << next << "->";
next = collatz[next].next;
}
cout << 1 << endl;
}
}
void printSteps(unsigned long long max) {
cout << "n,steps" << endl;
for(unsigned long long i=1;i<=max;i++) {
cout << i << "," << collatz[i].steps << endl;
}
}
int main(int argc, char* argv[]) {
struct element e;
e.next = 4;
e.steps = 0;
collatz[1] = e;
unsigned long long maxCollatz = (unsigned long long) atoi(argv[1]);
for (unsigned long long i = 2; i <= maxCollatz; i++) {
insertCollatz(i);
saveULong = i;
if (i % 1000000 == 0) {
cerr << i << endl;
}
}
cerr << "maxAddFromOneEntry: " << maxAddFromOneEntry << endl;
cerr << "maxStepsToOne: " << maxStepsToOne << endl;
cerr << "maxEntry: " << maxEntry << endl;
cerr << "entries: " << collatz.size() << endl;
//printCollatz();
printSteps(maxCollatz);
return 0;
}
Then I've processed it with R:
R -f analyze.R
analyze.R:
library(ggplot2)
memory.limit(4000)
mydata = read.csv("/home/moose/Downloads/algorithms/collatz/steps.csv")
# Prepare data
p<-ggplot(mydata, aes ( x=n,y=steps ))
p<-p + geom_hex(bins=30)
p<-p + opts(panel.background = theme_rect(fill='white', colour='white'))
# This will save the result in a pdf file called Rplots.pdf
p
And finally, I've converted it to png:
inkscape Rplots.pdf -w 512 --export-png=collatz-sequence-steps.png
I've explained this a bit more detailed on StackExchange.
Maximum in sequence
In the following plot you can see \(n \in 1, \dots, 10,000,000\) on the \(x\)-axis and the maximum \(y = \max(\{a^n_i | i \in \mathbb{N}_{> 0}\})\):
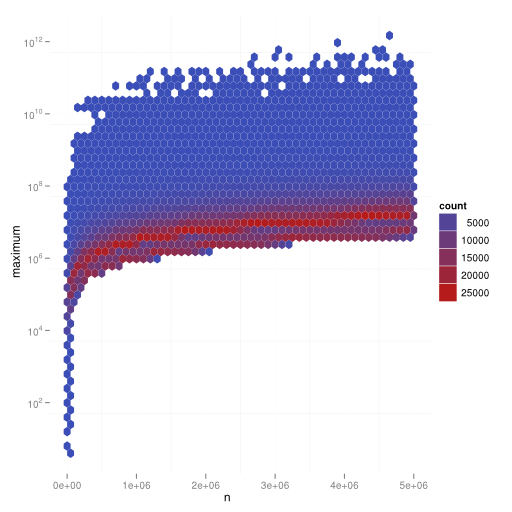
library(ggplot2)
mydata = read.csv("../collatz-maxNumber.csv")
# Prepare data
p<-ggplot(mydata, aes(x=n, y=maximum)) + scale_y_log10()
p<-p + geom_hex(bins=50)
p<-p + opts(panel.background = theme_rect(fill='white', colour='white'))
# This will save the result in a pdf file called Rplots.pdf
p
Execution times
Generating all Collatz sequences up to 10,000,000 items took about 50 seconds. But R needed about 10 minutes to generate images from that.
Inkscape didn't like the heavy plot:
moose@pc07$ inkscape Rplots.pdf -w 512 --export-png=maxInSequence.png
(inkscape:26733): GLib-ERROR **: /build/buildd/glib2.0-2.34.1/./glib/gmem.c:165: failed to allocate 3440640 bytes
^CTrace/breakpoint trap (core dumped)
Maximum in sequence and steps
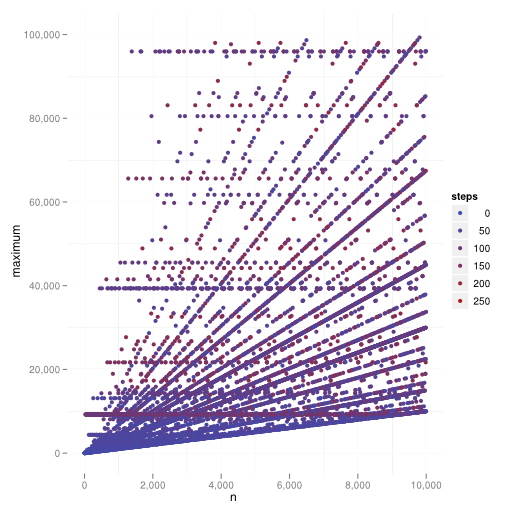
Read more
- All sources of this article are on GitHub
- Dot guide, Node shapes
- R on UbuntuUsers (German)
- Project Euler 14