Machine Learning 1

Dieser Artikel beschäftigt sich mit der Vorlesung „Machine Learning 1“ am KIT. Er dient als Prüfungsvorbereitung. Ich habe die Vorlesungen bei Herrn Prof. Dr. Zöllner im Wintersemester 2014/2015 gehört.
Es gibt auch einen Artikel über Machine Learning 2.

Folien

Einordnungskriterien

Slide name: ML-Einordnungskriterien.pdf

Algorithmus Inferenztyp Lernebene Lernvorgang Beispielgebung Beispielumfang Hintergrundwissen
ind. ded. symb. subsymb. überwacht unüb. inkr. nicht inkr. gering groß emp. axio.
$k$-NN x     x x     x   x x  
SVMs x     x x     x   x x  
Decision Trees ID3 x   x   x     x   x x  
ID5R x   x   x   x     x x  
NN klassisch x     x x     x   x x  
Auto-Encoder x     x   x   x   x x  
Bayessche Netze x     x x     x   x x  
HMMs x     x x     x   x x  
Version-Space Algorithmus x   x   x   x     x x  
Specific-to-General Konzeptlernen ? ? x   ? ? ? ? ? ? ? ?
k-means clustering x     x   x   x   x x  
AHC x     x   x   x   x x  
COBWEB x   x     x x   x   x  
CBR x   x   x   x   x   x  
EBG   x x   x   x   x     x

Einführung

Slide name: MLI_01_Einfuehrung_slides1.pdf

  • Was ist Intelligenz? (Problemlösen, Erinnern, Sprache, Kreativität, Bewusstsein, Überleben in komplexen Welten, )
  • Wissensrepräsentation:
    • Assoziierte Paare (Eingangs- und Ausgangsvariablen)
    • Entscheidungsbäume (Klassen diskriminieren)
    • Parameter in algebraischen ausdrücken
    • Formale Grammatiken
    • Logikbasierte Ausdrücke
    • Taxonomien
    • Semantische Netze
    • Markov-Ketten
Machine Learning von Tom Mitchell
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
Deduktion
Die Deduktion ist eine Schlussfolgerung von gegebenen Prämissen auf die logisch zwingenden Konsequenzen. Deduktion ist schon bei Aristoteles als „Schluss vom Allgemeinen auf das Besondere“ verstanden worden.
Modus ponens
Der Modus ponens ist eine Art des logischen Schließens. Er besagt: Wenn die Prämissen $A \rightarrow B$ und $A$ gelten, dann gilt auch $B$.
Abduktion by Peirce
Deduction proves that something must be; Induction shows that something actually is operative; Abduction merely suggests that something may be.

Induktives Lernen

Slide name: MLI_02_InduktivesLernen_slides1.pdf

Version Space
Der Raum aller Hypotesen, welche mit den Trainingsbeispielen konsistent sind.
Version Space Algorithmus
Der Version Space Algorithmus ist ein binärer Klassifikator für diskrete Feature-Spaces. Er startet mit der generellsten Hypothese $G = (?, \dots, ?)$ - alles ist wahr - und der speziellsten Hypothese $S = (\#, \dots, \#)$ - nichts ist wahr. Wenn ein Beispiel mit dem Label true gesehen wird, dann wird die speziellste Hypothese angepasst und veralgemeinert. Wenn ein Beispiel mit dem Label false gesehen wird, wird die generellste Hypothese spezialisiert.
So kann man den Raum aller mit den Trainingsdaten konsistenten Hypothesen finden.
Konzept
Ein Konzept beschreibt eine Untermenge von Objekten oder Ereignissen definiert auf einer größerer Menge.
Konsistenz
Keine negativen Beispiele werden positiv klassifiziert.
Vollständigkeit
Alle positiven Beispiele werden als positiv klassifiziert.
  • Algorithmen: Bäume (Wälder?)
    • Suche vom Allgemeinen zum Speziellen: Negative Beispiele führen zur Spezialisierung
    • Suche vom Speziellen zum Allgemeinen: Positive Beispiele führen zur Verallgemeinerung
    • Version Space: Beides gleichzeitig anwenden
  • Präzendenzgraphen: In welcher Reihenfolge werden Aktionen ausgeführt?

Version Space Algorithmus ist:

  • Induktiver Inferenztyp
  • Symbolische Ebene des Lernens
  • Überwachtes Lernen
  • Inkrementelle Beispielgebung
  • Umfangreich (viele Beispiele)
  • Empirisches Hintergrundwissen
  • Voraussetzungen: Konsistente Beispiele, korrekte Hypothese im Hypothesenraum
  • Positive Aspekte:
  • Es ist feststellbar, welche Art von Beispielen noch nötig ist
  • Es ist feststellbar, wann das Lernen abgeschlossen ist

Weiteres

Inductive bias
Induktives Lernen benötigt Vorannahmen.
Bias ("Vorzugskriterium")
Vorschrift, nach der Hypothese gebildet werden.

Reinforcement Learning

Slide name: MLI_03_ReinforcementLearning_slides1.pdf

Siehe auch:

Markovsches Entscheidungsproblem (Markov Decision Process, MDP)
Ein Markovsches Entscheidungsproblem ist ein 5-Tupel $(S, A, P, R, p_0)$, wobei
  • $S$ eine endliche Zustandsmenge (states),
  • $A(s)$ eine Menge von möglichen Aktionen im Zustand $s$,
  • $P(s, s', a) = P(s_{t+1} = s' | s_t = s, a_t = a)$: Die Wahrscheinlichkeit im Zeitschritt $t+1$ im Zustand $s'$ zu sein, wenn man zum Zeitpunkt $t$ im Zustand $s$ ist und die Aktion $a$ ausführt
  • $R(s, s', a) \in \mathbb{R}$: Die direkte Belohnung, wenn durch die Aktion $a$ vom Zustand $s$ in den Zustand $s'$ gekommen ist.
  • $p_0$ ist die Startverteilung auf die Zustände $S$
Manchmal wird auch der Diskontierungsfaktor $\gamma \in [0, 1]$, welche die Bedeutung von direkten Belohnungen im Vergleich zu künftigen Belohnungen anzeigt, hier schon genannt. Allerdings finde ich das an dieser Stelle eher unpassend, da $\gamma$ eher verwendet wird um die Lösung in der Praxis bestimmen zu können. Mit dem Problem hat $\gamma$ an sich nichts zu tun.
Reinforcement Learning (RL, Bestärkendes Lernen)
Beim bestärkenden Lernen liegt ein Markow-Entscheidungsproblemen vor. Es gibt also einen Agenten, der Aktionen ausführen kann. Diese können (nicht notwendigerweise sofort) bewertet werden.
Policy (Strategie)
Siehe Probabilistische Planung.
Policy Learning
Unter Policy Learning versteht man die Suche nach einer optimalen Strategie $\pi^*$.
V-Funktion (Value function, State-Value function)
Die Funktion $V^\pi: S \rightarrow \mathbb{R}$ heißt Value-Funktion. Sie gibt den erwarteten Wert (nicht die Belohnung, da bei der V-Funktion noch der Diskontierungsfaktor eingeht!) eines Zustands $s$ unter der Strategie $\pi$ an.

Mit $V^*$ wird der Wert unter der optimalen Strategie bezeichnet.
Q-Funktion (Action-Value function, Quality function)
Siehe Probabilistische Planung.
Eligibility Traces
Siehe Probabilistische Planung.
  • Beispiel für RL: Roboter muss zu einem Ziel navigieren

Algorithmen:

Simple Value Iteration
Simple Value Iteration estimates the value function by updating it as long as necessary to converge: $$\hat{V}^*(s_t) \leftarrow r_t + \gamma \hat{V}^*(s_{t+1})$$ "Simple" means that the transition function is deterministic. It is explained in
Simple Temporal Difference Learning
Simple Temporal Difference Learning is just like Simple Value Iteration, but now the Value function is updated with a learning rate $\alpha$: $$\hat{V}^*(s_t) \leftarrow (1-\alpha) \cdot \hat{V}^*(s_t) + \alpha(r_t + \gamma \hat{V}^*(s_{t+1}))$$ Mehr dazu im nächsten Abschnitt.
Q-Learning
Siehe Probabilistische Planung.
SARSA (State-Action-Reward-State-Action)
Siehe Probabilistische Planung.
SARSA($\lambda$)
Siehe Probabilistische Planung.

TD-Learning

Der TD-Learning Algorithmus beschäftigt sich mit dem Schätzen der Value-Funktion \(V^\pi\) für eine gegebene Strategie \(\pi\). Das wird auch policy evaluation oder prediction genannt.

Siehe auch

Lerntheorie

Slide name: MLI_04_Lerntheorie_slides1.pdf

Ockhams Rasiermesser (Quelle: Wikipedia)
Von mehreren möglichen Erklärungen für ein und denselben Sachverhalt ist die einfachste Theorie allen anderen vorzuziehen. Eine Theorie ist einfach, wenn sie möglichst wenige Variablen und Hypothesen enthält, und wenn diese in klaren logischen Beziehungen zueinander stehen, aus denen der zu erklärende Sachverhalt logisch folgt.
Overfitting
Zu starke Anpassung des Klassifizierers an die Lerndaten; geringe Generalisierungsfähgikeit
Structural Risc Minimization (SRM)
Unter Structural risk minimization versteht man die Abwägung zwischen einem einfachen Modell und einem komplexen Modell, welches auf den Trainingsdaten besser funktioniert aber eventuell mehr unter Overfitting leidet.
Vapnik-Chervonenkis Dimension (VC-Dimension)
Die VC-Dimension $VC(H, X) \in \mathbb{N} \cup \infty$ eines Hypothesenraumes $H$ ist gleich der maximalen Anzahl an Datenpunkten aus $X$, die von $H$ beliebig in zwei Mengen gespalten werden können. Dabei muss es nur eine Teilmenge $X' \subseteq X $ der Größe $n$ geben, damit $VC(H, X) \geq n$ gilt. Falls beliebige Teilmengen von $X$ durch $H$ separiert werden können, so gilt $VC(H, X) = \infty$. Praktisch gesehen ist $X$, die Menge aller möglichen Features, sowie $H$, die Menge aller möglichen Trennlinien im Feature-Space, vorgegeben. Die Frage ist ob man eine Teilmenge $X' \subseteq X$ findet mit $|X'| = n$, sodass man für $X'$ jede Mögliche Teilung in zwei Mengen durch $H$ realisieren kann.
Probably approximately correct learning (PAC)
PAC macht eine Aussage über die Anzahl der benötigten Stichproben, wenn man einen bestimmten realen Fehler mit einer frei zu wählenden Wahrscheinlichkeit bekommen will.
  • Lernmaschine wird definiert durch Hypothesenraum \(\{h_\alpha: \alpha \in A\}\) und Lernverfahren. Das Lernverfahren ist die Methode um \(\alpha_{\text{opt}}\) mit Hilfe von Lernbeispielen zu finden.
  • Probleme beim Lernen:
    • Größe des Hypothesenraums im Vergleich zur Anzahl der Trainingsdaten.
    • Das Verfahren könnte nur suboptimale Lösungen finden.
    • Das Verfahren könnte die passende Hypothese nicht beinhalten.
  • Lernproblemtypen: Sei die Menge der Lernbeispiele in \(X \times Y\), mit \(X \times Y =\)...
    • \(\{Attribut_1, Attribut_2, ...\} \times \{True, False\}\): Konzeptlernen
    • \(\mathbb{R}^n \times \{Klasse_1, ..., Klasse_n\}\): Klassifikation
    • \(\mathbb{R}^n \times \mathbb{R}\): Regression
  • Gradientenabstieg, Overfitting
  • Kreuzvalidierung
  • PAC
    • Folie 35: Was ist eine Instanz der Länge \(n\)?
      Eine Hypothese mit \(n\) Literalen.

Boosting

Boosting
Kombiniere mehrere schwache Modelle um ein gutes zu bekommen, indem Trainingsbeispiele unterschiedlich gewichtet werden.
Bagging (Bootstrap aggregating)
Kombiniere mehrere schwache Modelle um ein gutes zu bekommen. Dabei bekommt jedes schwache Modell nur eine Teilmenge aller Trainingsdaten.
AdaBoost (Adaptive Boosting; see YouTube)
Learn a classifier for data. Get examples where the classifier got it wrong. Train new classifier on the wrong ones.
  • Folie 22:
    • Wofür steht \(i\) und welchen Wertebereich hat \(i\)?
      → \(i\) ist eine Zählvariable, welche die Trainingsdaten durchnummeriert.
    • Stellt \(W_k(i)\) die Wahrscheinlichkeit dar, dass Beispiel \(i\) im \(k\)-ten Durchlauf für das Training verwendet wird?
      → Nein. \(W_k(i)\) ist das Gewicht des \(i\)-ten Trainingsbeispiels für den \(k\)-ten klassifikator. Siehe Folie 24 und folgende für ein Beispiel.

Siehe auch:

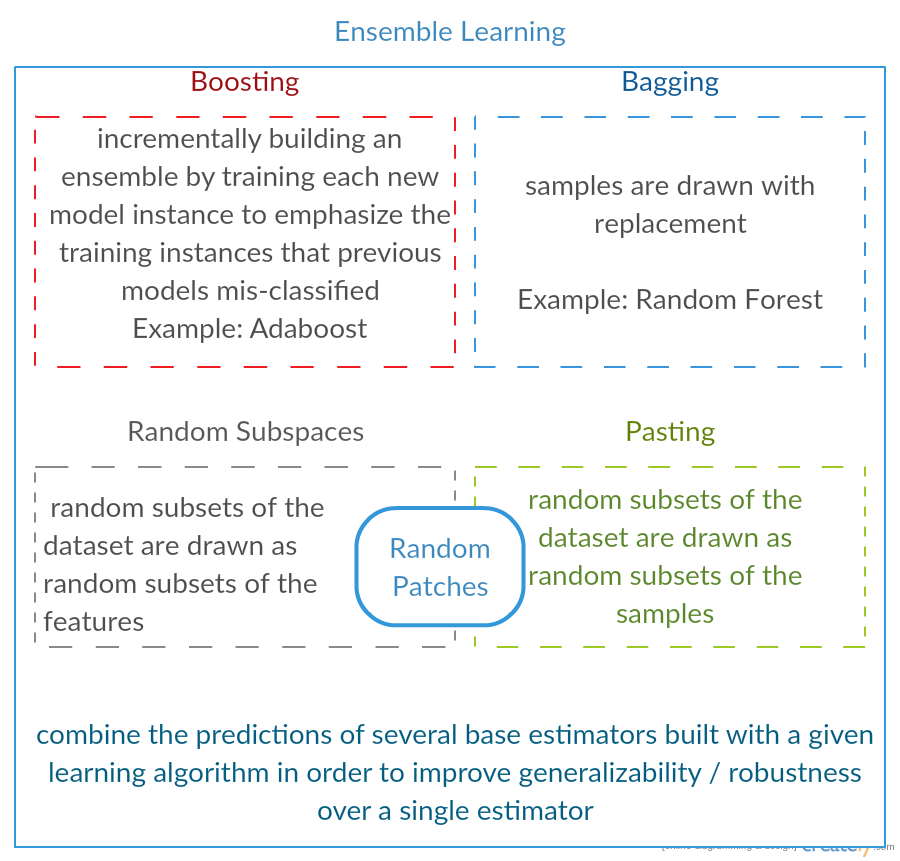
Ensemble Learning Techniques: Boosting, Bagging, Random Subspaces, Pasting, Random Patches
Ensemble Learning Techniques: Boosting, Bagging, Random Subspaces, Pasting, Random Patches

Weiteres:

Stacking
A committee learner, usually OLS or LASSO
Bagging/Bragging
Learnier is fit, results are mean/median aggregated with the aim of reduction variance
Boosting
Build chain of learners.

VC-Dimension

VC-Dimension, siehe YouTube und [Mit97]
Sei $H^\alpha = \{h_\alpha : \alpha \in A\}$ der Hypothesenraum. Die VC-Dimension $VC(h_\alpha)$ von $H^\alpha$ ist gleich der maximalen Anzahl von beliebig platzierten Datenpunkten, die von $H^\alpha$ separiert werden können.

Neuronale Netze

Slide name: MLI_05_Neuronale_Netze_slides1.pdf

  • Einsatzfelder:
    • Klassifiktion: Spracherkennung, Schrifterkennung
    • Funktionsapproximation
    • Mustervervollständigung: Kodierung, Bilderkennung (NODO: Warum zählt das nicht zu Klassifikation?)
  • Perzeptron von Rosenblatt (1960)
    • Auswertung: Input-Vektor und Bias mit Gewichten multiplizieren, addieren und Aktivierungsfunktion anwenden.
    • Training: Zufällige Initialisierung des Gewichtsvektors, addieren von fehlklassifizierten Vektoren auf Gewichtsvektor.
  • Gradientenabstieg
  • Software:
  • Lasagne: Python, hat eine exzellente Dokumentation, die auch größtenteils auf explizit auf Literatur verweist und die Formeln hinter den Funktionen direkt angibt.
  • Google TensorFlow
Cascade Correlation (siehe Fahlman und Lebiere: The Cascade-Correlation Learning Architecture)
Cascade Correlation ist ein konstruktiver Algorithmus zum erzeugen von Feed-Forward Neuronalen Netzen. Diese haben eine andere Architektur als typische multilayer Perceptrons. Bei Netzen, welche durch Cascade Correlation aufgebaut werden, ist jede Hidden Unit mit den Input-Neuronen verbunden, mit den Output-Neuronen und mit allen Hidden Units in der Schicht zuvor.

Siehe YouTube (4:05 min) und How exactly does adding a new unit work in Cascade Correlation?
RPROP (siehe YouTube - 15:00min)
Rprop ist eine Gewichtsupdate-Regel für neuronale Netze. Sie betrachtet nur das Vorzeichen des Gradienten, jedoch nicht den Betrag. Jedes Gewicht wird unabhängig von den anderen behandelt. Der Algorithmus hat Konstanten $\eta^- \in \mathbb{R}_{\le 1}$ sowie $\eta^+ \in \mathbb{R}_{\ge 1}$. Für jedes Gewicht ist außerdem $\eta=1$ zu Beginn. Bei jedem Gewichtsupdate wird überprüft, ob sich das Vorzeichen des Gradienten für dieses Gewicht geändert hat. Falls ja, wird das Gewicht um $\eta \cdot \eta^+$ bzw $\eta \cdot \eta^-$ geändert. Außerdem kann eine minimale bzw. eine Maximale Änderung gesetzt werden.
Delta-Regel, siehe neuronalesnetz.de
Die Delta-Regel ist ein Lernalgorithmus für neuronale Netze mit nur einer Schicht. Sie ist ein Spezialfall des algemeineren Backpropagation-Algorithmus und lautet wie folgt: $$\Delta w_{ji} = \alpha (t_j - y_j) \varphi'(h_j) x_i$$ wobei
  • $\Delta w_{ji} \in \mathbb{R}$ die Änderung des Gewichts von Input $i$ zum Neuron $j$,
  • $\alpha \in [0, 1]$ die Lernrate (typischerweise $\alpha \approx 0.1$),
  • $t_j \in \mathbb{R}$ der Zielwert des Neurons $j$,
  • $y_j \in \mathbb{R}$ die tatsächliche Ausgabe,
  • $\varphi'$ die Ableitung der Aktivierungsfunktion des Neurons,
  • $h_j \in \mathbb{R}$ die gewichtete Summe der Eingaben des Neurons und
  • $x_i \in \mathbb{R}$ der $i$-te Input
ist.
Gradient-Descent Algorithmus
Der Gradient-Descent Algorithmus ist ein Optimierungsalgorithmus für differenzierbare Funktionen. Er startet an einer zufälligen Stelle $x_0$. Dann wird folgender Schritt mehrfach ausgeführt: $$x_0 \gets x_0 - \alpha \cdot \text(grad) f (x_0)$$ wobei $\alpha \in (0, 1]$ die Lernrate ist und $f$ die zu optimierende Funktion. Dabei könnte $\alpha$ mit der Zeit auch kleiner gemacht werden.
Backpropagation (siehe neuralnetworksanddeeplearning.com)
Der Backpropagation-Algorithmus ist eine Variante des Gradient-Descent Algorithmus, welche für MLPs angepasst wurde. Sie besteht aus drei Schritten:
  • Forward-Pass: Lege die Input-Features an das Netz an und erhalte den Output
  • Fehlerberechnung: Mache das für alle Daten
  • Backward-Pass: Passe die Gewichte
Im Grunde ist Backpropagation nur eine Geschwindigkeitsoptimierte Variante des Gradient-Descent Algorithmus, da die Gradienten im Backpropagation-Algorithmus auf geschickte Weise berechnet werden.
Radiale Basisfunktion (Radial Basis Function, RBF)
Eine radiale Basisfunktion ist eine Funktion $f: D \rightarrow \mathbb{R}$, für die $f(x) = f(\|x\|)$ gilt bzw. allgemeiner, für die ein $c \in D$ existiert, sodass $f(x, c) = f(\|x - c\|)$ gilt. Der Wert der Funktion hängt also nur von der Distanz zum Ursprung bzw. allgemeiner zu einem Punkt $c \in D$ ab. Ein typisches Beispiel sind gaußsche RBFs: $f(x) = e^{-(a (x - c)^2)}$, wobei $a, c$ Konstanten sind.
Radial-Basis Funktion Netz (RBF-Netz)
Ein Radial-Basis Funktion Netz ist eine neuronales Netz, welches als Aktivierungsfunktionen RBFs verwendet. Dabei gibt es dann für jedes Neuron im Grunde zwei Parameter: Der Radius und das Zentrum (vgl. Folie 39 für die Gewichtsanpassung).
Dynamic Decay Adjustment (DDA)
DDA ist ein konstruktiver Lernalgorithmus für RBF-Netze welcher in [Ber95] vorgestellt wird. Bei den Netzwerken, die DDA annimmt, gibt es sog. Prototypen. Das scheinen einfach Neuronen mit RBF-Aktivierungsfunktionen zu sein, welche für eine Klasse stehen. Zwei Schwellwerte, $\theta^+$ und $\theta^-$, werden eingeführt. Der Schwellwert $\theta^+$ muss beim Training eines Beispiels der Klasse $y_1$ von einem Neuron der Klasse $y_1$ überschritten werden. Falls das nicht der Fall ist, wird ein neues Neuron hinzugefügt.
Der Schwellwert $\theta^-$ ist eine obere Grenze für die Aktivierung von Neuronen, die zu anderen Klassen gehören. Ist eine Aktivierung höher, wird der Radius des zugehörigen Neurons verringert.
$\theta^+ = 0.4$ und $\theta^- = 0.2$ sind sinnvolle Werte.
Laut einem Prüfungsprotokoll lernt DDA nach Vapnik korrekt.

Siehe auch: The Dynamic Decay Adjustment Algorithm

Siehe auch

Instanzbasiertes Lernen

Slide name: MLI_06_InstanzbasiertesLernen_slides1.pdf

Instanzenbasiertes Lernen bzw. Lazy Learning
Instanzenbasiertes Lernen ist ein Lernverfahren, welches einfach nur die Beispiele abspeichert, also faul (engl. lazy) ist. Soll der Lerner neue Daten klassifizieren, so wird die Klasse des ähnlichsten Datensatzes gewählt.
Case-based Reasoning bzw. kurz CBR
CBR ist ein allgemeines, abstraktes Framework und kein direkt anwendbarer Algorithmus. Die Idee ist, dass nach ähnlichen, bekannten Fällen gesucht wird, auf die der aktuelle Fall übertragen werden kann.
Fall im Kontext des CBR
Ein Fall ist eine Abstraktion eines Ereignisses, die in Zeit und Raum begrenzt ist. Ein Fall enthält eine Problembeschreibung, eine Lösung und ein Ergebnis. Zusätzlich kann ein Fall eine Erklärung enthalten warum das Ergebnis auftrat, Informationen über die Lösungsmethode, Verweise auf andere Fälle oder Güteinformationen enthalten.

  • Beispiel für Lazy Learning: \(k\)-NN, CBR

  • NODO: Folie 3: „Fleißige“ Lernalgorithmen mit dem gleichen Hypothesenraum sind eingeschränkter - was ist damit gemeint? Was sind fleißige Lernalgorithmen? Lernalgorithmen, welche den meisten Rechenaufwand beim Lernen investieren, wo aber das auswerten vergleichsweise billig ist?

SVM

Slide name: MLI_07_SVM_slides1.pdf

Eine Erklärung von SVMs findet sich im Artikel Using SVMs with sklearn.

  • SVMs sind laut Vapnik die Lernmaschine mit der kleinsten möglichen VC- Dimension, falls die Klassen linear trennbar sind.
  • Primäres Optimierungsproblem: Finde einen Sattelpunkt der Funktion
    \(L_P = L(\vec{w}, b, \vec{\alpha}) = \frac{1}{2}\|\vec{w}\|^2 - \sum_{i=1}^N \alpha_i (y_i(\vec{w}\vec{x_i}+b)-1)\) wobei \(\alpha_1, \dots, \alpha_N \geq 0\) Lagrange-Multiplikatoren sind
  • Soft Margin Hyperebene
  • Der Parameter \(C\) dient der Regularisierung. Ist \(C\) groß gibt es wenige Missklassifikationen in der Trainingsdatenmenge. Ist \(C\) klein, werden die Margins größer.
  • Nichtlineare Kernelmethoden
  • Kernel-Trick

Abschätzung des realen Fehlers

Der reale Fehler kann durch den empirischen Fehler und die VC-Dimension wie folgt abgeschätzt werden: Mit Wahrscheinlichkeit $P(1-\eta)$ gilt: $$E(h_\alpha) \leq E_{emp}(h_\alpha) + \sqrt{\frac{VC(h_\alpha)}{N} \cdot (\log(2 N / VC(h_\alpha)) + 1) - \frac{\log(\eta / 4)}{N}}$$ wobei gilt:
  • $E(h_\alpha)$ ist der reale Fehler der mit der Hypothese $h_\alpha$ gemacht wird
  • $E_{emp}(h_\alpha)$ ist der empirische Fehler der mit der Hypothese $h_\alpha$ gemacht wird
  • $VC(h_\alpha)$ ist die VC-Dimension der Lernmaschine
  • $N$ ist die Anzahl der Lernbeispiele
  • $0 \leq \eta \leq 1$
Dieser Term wird in der Structural Risc Minimization minimiert.

Entscheidungsbäume

Slide name: MLI_08_Entscheidungsbaeume_slides1.pdf

Entscheidungsbaum (Decision Tree)
Ein Entscheidungsbaum ist ein Klassifikator in Baumstruktur. Die inneren Knoten des Entscheidungsbaumes sind Attributtests, die Blätter sind Klassen.

Typischerweise wird ein Entscheidungsbaum aufgebaut, indem das jeweilige Attribut mit dem höchsten Information Gain als nächster Knoten hinzugefügt wird. Siehe Information gain in decision trees für weitere Informationen.
ID3 (siehe pseudocode)
ID3 ist ein Top-Bottom Verfahren zum Aufbau eines Entscheidungsbaumes.
C4.5 (siehe pseudocode)
ID3 ist ein Top-Bottom Verfahren zum Aufbau eines Entscheidungsbaumes, welches auf ID3 basiert.
Random Forest, Quelle: Wikipedia
Ein Random Forest ist ein Klassifikationsverfahren, welches aus mehreren verschiedenen, unkorrelierten Entscheidungsbäumen besteht. Alle Entscheidungsbäume sind unter einer bestimmten Art von Randomisierung während des Lernprozesses gewachsen. Für eine Klassifikation darf jeder Baum in diesem Wald eine Entscheidung treffen und die Klasse mit den meisten Stimmen entscheidet die endgültige Klassifikation.
  • Der Algorithmus ID5R dienen dem Aufbau eines Entscheidungsbaumes.
  • C4.5 unterstützt - im Gegensatz zu ID3 - kontinuierliche Attributwerte. Außerdem kann C4.5 mit fehlenden Attributwerten umgehen.
  • Mögliches Qualtitätsmaß ist Entropie:
    \(Entropie(S) = - p_\oplus \log_2 p_\oplus - p_\ominus \log_2 p_\ominus\) wobei \(\oplus\) die positiven Beispiele und \(\ominus\) die negativen Beispiele bezeichnet.
  • Folie 41: Wo ist der Vorteil von ID5R im Vergleich zu ID3, wenn das Ergebnis äquivalent ist?
    → ID5R kann inkrementell verwendet werden. Es ist bei ID5R - im Gegensatz zu ID3 - also nicht nötig bei neuen Trainingsdaten neu zu trainieren.
  • Random Forest: Erstelle mehrere Entscheidungsbäume mit einer zufälligen Wahl an Attributen. Jeder Baum stimmt für eine Klasse und die Klasse, für die die meisten Stimmen, wird gewählt.

Bayes Lernen

Slide name: MLI_09_BayesLernen_slides1.pdf

Siehe auch:

Satz von Bayes
Seien $A, B$ Ereignisse, $P(B) > 0$. Dann gilt: $P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}$
Dabei wird $P(A)$ a priori Wahrscheinlichkeit, $P(B|A)$ likelihood, und $P(A|B)$ a posteriori Wahrscheinlichkeit genannt.
Naiver Bayes-Klassifikator
Ein Klassifizierer heißt naiver Bayes-Klassifikator, wenn er den Satz von Bayes unter der naiven Annahme der Unabhängigkeit der Features benutzt.
Produktregel
$P(A \land B) = P(A|B) \cdot P(B) = P(B|A) \cdot P(A)$
Summenregel
$P(A \lor B) = P(A) + P(B) - P(A \land P)$
Theorem der totalen Wahrscheinlichkeit
Es seien $A_1, \dots, A_n$ Ereignisse mit $i \neq j \Rightarrow A_i \cap A_j = \emptyset \;\;\;\forall i, j \in 1, \dots, n$ und $\sum_{i=1}^n A_i = 1$. Dann gilt:
$P(B) = \sum_{i=1}^n P(B|A_i) P(A_i)$
Maximum A Posteriori Hypothese (MAP-Hypothese)
Sei $H$ der Raum aller Hypothesen und $D$ die Menge der beobachteten Daten. Dann heißt
$h_{MAP} = \text{arg max}_{h \in H} P(h|D) \cdot P(h)$
die Menge der Maximum A Posteriori Hypothesen.
Maximum Likelihood Hypothese (ML-Hypothese)
Sei $H$ der Raum aller Hypothesen und $D$ die Menge der beobachteten Daten. Dann heißt
$h_{ML} = \text{arg max}_{h \in H} P(h|D)$
die Menge der Maximum Likelihood Hypothesen.
Normalverteilung
Eine stetige Zufallsvariable $X$ mit der Wahrscheinlichkeitsdichte $f\colon\mathbb{R}\to\mathbb{R}$, gegeben durch
$f(x) = \frac {1}{\sigma\sqrt{2\pi}} e^{-\frac {1}{2} \left(\frac{x-\mu}{\sigma}\right)^2}$
heißt $\mathcal N\left(\mu, \sigma^2\right)$-verteilt, normalverteilt mit den Erwartungswert $\mu$ und Varianz $\sigma^2$.
Prinzip der minimalen Beschreibungslänge
Das Prinzip der minimalen Beschreibungslänge ist eine formale Beschreibung von Ockhams Rasiermesser. Nach diesem Prinzip werden Hypothesen bevorzugt, die zur besten Kompression gegebener Daten führen.
Gibbs-Algorithmus (stats.stackexchange)
Der Algorithmus von Gibbs ist eine Methode um Stichproben von bedingten Verteilungen zu erzeugen.
Bedingte Unabhängigkeit
Seien $X, Y, Z$ Zufallsvariablen. Dann heißt $X$ bedingt unabhängig von $Y$ gegeben $Z$, wenn $$P(X|Y,Z) = P(X|Z)$$ gilt.
Add $k$ smoothing
Unter Add-$k$-smoothing versteht man eine Technik, durch die sichergestellt wird, dass die geschätzte Wahrscheinlichkeit für kein Ereignis gleich null ist. Wenn man $d \in \mathbb{N}$ mögliche Ergebnisse eines Experiments hat, $N \in \mathbb{N}$ experimente durchgeführt werden, dann schätzt man die Wahrscheinlichkeit von dem Ergebnis $i$ mit $$\hat{\theta_i} = \frac{x_i + k}{N+ kd}, $$ wobei $x_i$ die Anzahl der Beobachtungen von $i$ ist und $k \geq 0$ der Glättungsparameter ist.
Bayessches Netz (Quelle: [Dar09])
Ein bayessches Netz ist ein Tupel $(G, \Theta)$ mit:
  • $G = (\mathbf{X}, E)$ ist ein DAG der Struktur des Bayesschen Netzwerks genant wird. Dabei ist $\mathbf{X} = \{X_1, X_2, \dots, X_n\}$ die Menge der Knoten. Jeder Knoten entspricht einer Zufallsvariablen (z.B. Attribut).

    Existiert eine gerichtete Kante $(X_i, X_j) \in E$, so existiert eine direkte Abhängigkeit zwischen $X_i$ und $X_j$.
  • $\Theta$ ist die Menge der bedingten Wahrscheinlichkeitsverteilungen und heißt Parametrisierung des bayesschen Netzwerks. Es existiert für jedes $X_i$ genau eine Verteilung in $\Theta$, welche in Abhängigkeit der Elternknoten beschrieben wird.
In einem bayesschem Netz berechnet sich die gemeinsame Verteilung wie folgt: $$P(X_1, \dots, X_N) = \prod_{i=1}^N P(X_i | \text{Eltern}(X_i))$$ Die Modelierung von Bayesschen Netzen erfolgt meist durch den Menschen mit Expertenwissen. Alternativ kann die Struktur durch MCMC bestimmt werden. Sobald die Struktur gegeben ist wird die Menge der Verteilungen $\Theta$ durch den Expectation Maximization Algorithmus bestimmt.

Fragen:

HMM

Slide name: MLI_10_HMM_slides1.pdf

Markov-Bedingung (Beschränkter Horizont)
$P(q_{t+1}=S_{t+1}|q_t = S_t, q_{t-1} = S_{t-1}, \dots) = P(q_{t+1}=S_{t+1}|q_t = S_t)$
Hidden Markov Modell (HMM)
Eine HMM ist ein Tupel $\lambda = (S, V, A, B, \Pi)$:
  • $S = \{S_1, \dots, S_n\}$: Menge der Zustände
  • $V = \{v_1, \dots, v_m\}$: Menge der Ausgabezeichen
  • $A \in [0,1]^{n \times n}$ = (a_{ij}): Übergangsmatrix, die die Wahrscheinlichkeit von Zustand $i$ in Zustand $j$ zu kommen beinhaltet
  • $B = (b_{ik})$ die Emissionswahrscheinlichkeit $v_k$ im Zustand $S_i$ zu beobachten
  • $\Pi = (\pi_i) = P(q_1 = i)$: Die Startverteilung, wobei $q_t$ den Zustand zum Zeitpunkt $t$ bezeichnet
Vorwärts-Algorithmus
Der Vorwärts-Algorithmus löst das Evaluierungsproblem. Er benutzt dazu dynamische Programmierung: Die Variablen $\alpha_t(i) = P(o_1 o_2 \dots o_t; q_t = s_i | \lambda)$ gibt die Wahrscheinlichkeit an zum Zeitpunkt $t \in 1 \leq t \leq T$ im Zustand $s_i \in S$ zu sein und die Sequenz $o_1 o_2 \dots o_t$ beobachtet zu haben. Diese werden rekursiv berechnet. Dabei beginnt man mit Zeitpunkt $t=1$, berechnet die Wahrscheinlichkeit $o_1$ beobachtet zu haben für jeden Zustand.
Die Wahrscheinlichkeit der beobachteten Sequenz, gegeben die HMM $\lambda$, ist dann einfach die Summe der $\alpha_i$ des letzten Zeitschritts.
Rückwärts-Algorithmus
Der Rückwärts-Algorithmus löst das Dekodierungsproblem. Er benutzt dazu dynamische Programmierung: Die Variablen $\beta_t(i) = P(o_{t+1} o_{t+2} \dots o_{T}|q_t = s_i, \lambda)$ geben die Wahrscheinlichkeit an, dass die Sequenz $o_{t+1} o_{t+2} \dots o_{T}$ beobachtet werden wird, gegeben das HMM $\lambda$ und den Startzustand $s_i$.
Forward-Backward Algorithm
Der Forward-Backward Algorithmus berechnet für jeden Zeitpunkt die Wahrscheinlichkeitsverteilung der Zustände. Dafür glättet er die Werte des Vorwärts- und des Rückwärts-Algorithmus: $$\gamma_t(i) = \frac{\alpha_t(i) \beta_t(i)}{P(O|\lambda)}$$ Er findet jedoch nicht die wahrscheinlichste Zustandssequenz.
Viterbi-Algorithmus
Löst P2:
Siehe How to apply the Viterbi algorithm
Baum-Welch-Algorithmus
Löst P3: Gegeben sei eine Trainingssequenz $O_{\text{train}}$ und ein Modell $$\lambda = \{S, V, A, B, \Pi\}$$ Gesucht ist ein Modell $$\bar \lambda = \text{arg max}_{\bar \lambda = \{S, V, \bar A, \bar B, \bar Pi\}} P(O_{\text{train}}|\lambda)$$ Der Baum-Welch-Algorithmus geht wie folgt vor:
  1. Bestimme $P(O_{\text{train}} | \lambda)$
  2. Schätze ein besseres Modell $\bar \lambda$: TODO - Genauer! (Folie 31 - 36)
Iteriere diese Schritte so lange, bis ein lokales Maximum gefunden wurde.
Ergodisches Modell
Unter dem ergodischen Modell versteht man im Kontext von HMMs die vollverbundene Topologie inclusive Schleifen.
Bakis-Modell (Links-nach-Rechts-Modell)
Unter dem Bakis-Modell versteht man im Kontext von HMMs eine Links-nach-Rechts Topologie, bei der maximal ein Zustand übersprungen werden kann. Das bedeutet, es gibt eine Ordnung über den Zuständen. Von einem Zustand $i$ kommt man in die Zustände $i, i+1, i+2$.

Die drei Probleme von HMMs sind

  • P1 - Evaluierungsproblem: Wie wahrscheinlich ist eine Sequenz \(\bf{o} = o_1 o_2 \dots o_T\) gegeben ein HMM \(\lambda\), also \(P(\bf{o}|\lambda)\).
  • P2 - Dekodierungsproblem: Finden der wahrscheinlichsten Zustandssequenz \(s_1, \dots, s_T\), gegeben eine Sequenz von Beobachtungen \(\bf{o} = o_1 o_2 \dots o_T\).
  • P3 - Lernproblem: Optimieren der Modellparameter

Anwendungen:

  • Gestenerkennung
  • Phonem-Erkennung

Markov Logik Netze

Slides: MLI_11-MLN_slides1

Markov Logik Netze sind Sammlungen von Tupeln aus Gewichten \(w_i\) und prädikatenlogischen Formeln. Die Idee hinter Markov Logik Netzen ist ein aufweichen der harten Bedingungen der Prädikatenlogik. Eine prädikatenlogische Formel ist entweder wahr oder falsch. Eine Formel in MLNs kann auch "meistens" erfüllt sein. Das wird durch das Gewicht repräsentiert.

Markov Logik Netze (MLN)
Ein Markov Logik Netz ist ein Menge aus Tupeln $L = (F_i, w_i)$, wobei $F_i$ eine Formel der Prädikatenlogik erster Ordnung und $w_i \in \mathbb{R}$ ein Gewicht ist. Ein MLN ist eine Schablone für ein MRF.
Markov Random Field (Markov Netzwerk, MRF)
Ein MRF ist ein ungerichtetes Probabilistisches Grafisches Modell.
MRFs sind zur Modellierung von Korrelation geeignet.
Verbundwahrscheinlichkeit in MLNs
$P(x) = \frac{1}{Z} \exp(\sum_{i} w_i f_i(x))$ wobei $f_i$ das $i$-te Feature und $w_i$ ein Gewicht ist. Beispielsweise könnte $$f_i(x) = f_i(\text{smoking}, \text{cancer}) = \begin{cases}1 &\text{if } \neg \text{smoking} \lor \text{cancer}\\ 0 &\text{otherwise}\end{cases}$$ gelten.
Inferenz in MLNs
MAP: \begin{align}\text{arg max}_y P(y | x) &= \frac{1}{Z} \exp(\sum_{i} w_i n_i(x, y))\\ &= \sum_{i} w_i n_i(x, y) \end{align}

Siehe auch:

Evolutionäre Algorithmen

Slides: MLI_12_EvolutionaereAlgorithmen_slides1.pdf

Siehe auch:

Individuum
Eine mögliche Hypothese
Population (Generation)
Hypothesenmenge
Erzeugung von Nachkommen
Generierung neuer Hypothesen durch Rekombination und Mutation
Fitness-Funktion
Die Fitness-Funktion ist das zu optimierende Kriterium. Sie beschreibt die Güte einer Hypothese.
Selektion
Auswahl der Hypothesen, welche die beste Problemlösung erzeugen.
Evolutionäre Strategien
Das Wissen wird durch reele Zahlen und Vektoren repräsentiert.
Genetische Programmierung
Das Wissen wird duch baumartige Strukturen repräsentiert.
Mutation
Unter Mutation versteht man die zufällige Änderung einzelner Gene. Beispiele:
  • Bit-Inversion: Zufällig Gleichverteilt pro Gen / Feste Anzahl, aber zufällige Gene
  • Translation: Verschieben von Teilsequenzen
  • Invertiertes Einfügen
  • Spezielle Mutationsoperatoren sind anwendungsspezifisch
Rekombination
Bei der Rekombination werden die Eigenschaften zweier Eltern gemischt. Dies kann Diskret passieren, wenn manche Gene von einem Elternteil übernommen werden und andere vom anderen Elternteil. Alternativ kann die Rekombination auch durch intermediäre Rekombination passieren. Das bedeutet, das ein Gen gemittelt wird.

Grundalgorithmus:

Fitness-Function f
Population p

while f(p) ≠ optimal:
    p_parents ← selection(p)
    p_children ← generate_children(p_parents)
    p ← p_parents + p_children
    fitness ← f(p)
    p ← selection_kill(p, fitness)

Probleme:

  • Genetischer Drift: Manche Individuen vermehren sich zufällig mehr als andere. Diese sind nicht unbedingt besser für das Problem geeignet.
  • Crowding, Ausreißerproblem: Fitte Individuen dominieren die Population. Das ist ein Problem wegen lokaler Maxima.

Mating:

  • Inselmodell: Die Evolution läuft weitgehend getrennt. Es passiert nur vereinzelt, dass Individuen der Inseln ausgetauscht werden.
  • Nachbarschaftsmodell: Nachkommen dürfen nur von Individuen erzeugt werden, die in ihrer Nachbarschaft die beste Fitness besitzen
  • Globales Modell: Alle dürfen sich mit allen verbinden.

Evolution:

  • Lamark'sche Evolution: Die Individuen ändern sich nach der Erzeugung. Sie lernen also. Dabei wird der Genotyp verändert und auch vererbt.
  • Baldwin'sche Evolution: Die Individuen ändern sich nach der Erzeugung, aber der Genotyp bleibt gleich
  • Hybride Verfahren: Es gibt sich verändernde und gleich bleibende Phänotypen.

Anwendungen:

  • Traveling Salesman
  • Flugplanoptimierung
  • Mischung von Kaffesorten
  • Cybermotten: Motten müssen optimales Muster finden, um sich vor einer Fläche weißen Rauschens zu verbergen.
  • Snakebot (Ivan Tanev) [Pro06]

Deduktives Lernen

Slides: MLI_13_DeduktivesLernen_slides1.pdf

Siehe auch: Formale Systeme

Modus Ponens
$$\frac{A, A \rightarrow B}{B}$$
Erklärungsbasiertes Lernen (EBL, Explanation Based Learning by [Mit97])
The key insight behind explanation-based generalization is that it is possible to form a justified generalization of a single positive training example provided the learning system is endowed with some explanatory capabilitie. In particular, the system must be able to explain to itself why the training example is an example of the concept under study. Thus, the generalizer is presumed to possess a definition of the concept under study as well as domain knowledge for constructing the required explanation.
Explanation Based Generalization (EBG)
EBG ist ein Prozess, bei dem implizites Wissen in explizites umgewandelt wird. EBG geht wie folgt vor:
  1. Explain: Finden einer Erklärung, warum das Beispiel die Definition des Zielkonzepts erfüllt. Dies ist einfaches Anwenden des Modus Ponens.
  2. Generalize: Generalisieren der Erklärung; bestimme also hinreichende Bedingungen unter denen die gefundene Erklärungsstruktur gültig ist.
Bei der EBG werden also Makro-Operatoren erzeugt. Ein Beispiel für Software welche EBG benutzt ist STRIPS.
KBANN (Knowledge-Based Artificial Neural Networks)
KBANN ist ein hybrides Verfahren. Die Idee ist ein neuronales Netz geschickt zu konstruieren. Dieses wird dann wie gewohnt mit Gradient Descent durch Trainingsbeispiele verfeinert. Der Algorithmus gibt eine Netzarchtiktur vor:
  • Dabei wird pro Instanzattribut ein Netz-Input verwendet. Für jede Klausel wird ein Neuron hinzugefügt.
  • Dieses ist mit dem Instanzattribut durch das Gewicht $w$ verbunden wenn es nicht negiert ist, sonst durch das Gewicht $-w$.
  • Der Schwellwert der Aktivierungsfunktion wird auf $-(n- 0.5)w$ gesetzt, wobei $n$ die Anzahl der nicht-negierten Bedingungsteile ist.
  • Verbinde die restlichen Neuronen von Schicht $i$ mit Schicht $i+1$ indem zufällige kleine Gewichte gesetzt werden.
Angewendet werden kann KBANN:
  • Lernen von physikalischen Objektklassen
  • Erkennung von biologischen Konzepten in DNS-Sequenzen

Unüberwachte Lernverfahren

Slides: MLI_14_UnueberwachtesLernen_slides1.pdf

$k$-means Clustering
Der $k$-means Clustering Algorithmus finden $k$ Cluster in einem Datensatz. Dabei ist $k \in \mathbb{N}_{\geq 1}$ vom Benutzer zu wählen. Zuerst initialisert $k$-means die Zentroiden, also zentrale Punkte für Cluster, zufällig. Dann geht $k$-means geht iterativ vor:
  1. Weise jeden Datenpunkt seinem nächsten Cluster zu.
  2. Verschiebe die $k$ Zentroide in ihr Clusterzentrum
Siehe auch: Interaktives Beispiel
Fuzzy $k$-means
Im Gegensatz zum $k$-means Algorithmus, wo jeder Datenpunkt in genau einem Cluster ist, weißt der Fuzzy $k$-means Algorithmus jedem Datenpunkte eine Zugehörigkeitswahrscheinlichkeit zu. Je weiter der Datenpunkt vom Zentroid entfernt ist, desto unwahrscheinlicher wird die Zugehörigkeit. Die Cluster-Zugehörigkeit des Datenpunktes $x_i$ zum Cluster $c_j$ kann als Wahrscheinlichkeit in Abhängigkeit der Distanz $$d_{ij} = |x_i - z_j|^2$$ zum Zentroiden $z_j$ ausgedrückt werden: $$P(c_j | x_i) = \frac{(\frac{1}{d_{ij}})^{\frac{1}{b-1}}}{\sum_{r=1}^k (\frac{1}{d_{ir}})^{\frac{1}{b-1}}}$$ wobei $b \in \mathbb{R}_{\geq 1}$ ein frei zu wählender Parameter ist. Die Zentroide werden dann wie folgt neu berechnet: $$z_j = \frac{\sum_{i=1}^n [P(z_j|x_i)]^b \cdot x_i}{\sum_{i=1}^n [P(z_j | x_i)]^b}$$
Hierarchisches Clustern
Die Idee des hierarchischen Clusterns ist die iterative Vereinigung von Clustern zu größeren Clustern. Ergebisse können durch ein Dendrogramm beschrieben werden. Anwendung: Einordnung von Schrauben in ein Ordnungssystem
Agglomerative Hierarchical Clustering (AHC)
AHC ist ein hierarchisches Clusteringverfahren. Dabei ist ein Clusterdistanz-Schwellwert $t \in \mathbb{R}$ und eine minimale Cluster-Anzahl $k \in \mathbb{N}$ zu wählen. Auch ein Distanzmaß für Cluster (nearest neighbor, farest neighor, mean distance, ...) ist als Hyperparameter zu wählen. Dann geht AHC wie folgt vor: 

c ← k  # Minimale Anzahl an Clustern
c' ← n  # Anzahl der Datenpunkte

# Weise jedem Punkt sein eigenes Clusterzentrum zu
for i in range(1, n):
    D_i ← {x_i}

# Vereinige Clusterzentren
do:
    c' := c' -1
    find closest clusters D_i, D_j
    if d(D_i, D_j) ⩽ t:
        merge(D_i, Dj)
    else:
        break
until c = c'
The result can be visualized as a Dendrogramm.
Begriffliche Ballung
Bei Algorithmen der Begrifflichen Ballung werden Konzeptbeschreibungen generiert.
COBWEB
Cobweb ist ein Algorithmus zur begrifflichen Ballung. Er lernt durch inkrementelles Aufbauen eines Strukturbaumes. Dabei sind nominale Attribute gestattet. Dabei wird ein Datenpunkt $x_i$ zum Cluster $c_j$ geclustert, wenn man die Attributwerte von $x_i$ durch die Kentniss von $c_j$ gut vorhersagen kann ($P(x_i | c_j)$, predictability) und zugleich der Cluster gut vorhergesagt werden kann, wenn die Attributwerte gegeben sind ($P(c_j|x_i)$, predictiveness). Es soll also in inter-Klassenähnlichkeit minimiert und die intra-Klassenähnlichkeit maximimiert werden. Dafür wird die Category Utility verwendet:
$$\text{CU} = \sum_{k=1}^K \sum_{i=1}^I \sum_{j=1}^{J(i)} P(A_i = V_{ij}) \cdot P(A_i = V_ij | C_k) \cdot P(C_k | A_i = V_{ij})$$
Dabei gilt:
  • $K$: Anzahl der Cluster
  • $I$: Anzahl der Attribute
  • $J(i)$: Anzahl der Attributwerte des $i$-ten Attributs
  • $V_{ji}$: $j$-ter möglicher Wert für Attribut $i$
  • $P(A_i = V_ij | C_k)$: Predictability
  • $P(C_k | A_i = V_{ij}$: Predictiveness
Anwendung: Interpretation von EMGs

Prüfungsfragen

  • Was ist Induktives Lernen?
    → Eine große Menge an Beispielen wird gegeben. Der Lerner muss selbst das Konzept herausfinden.
  • Was ist Deduktives Lernen?
    → Fakten werden gegeben. Der lernende bekommt das allgemeine Konzept gesagt und muss nur logische Schlussfolgerungen machen.
  • SVMs
    • Wie funktioniert SRM bei SVMs?
      → Dualität zwischen Feature- und Hypothesenraum: Radius der Hyperkugel wird minimiert.
    • Warum lernen SVMs "korrekt"?
      → Es gibt ein Theorem (TODO: Welches?) das besagt, dass die VC-Dimension eines Klassifiers, welcher Datenpunkte im $n$-Dimensionalen Raum innerhalb einer Kugel mit Radius $D$ durch eine Hyperebene mit mindestens Abstand $\Delta$ trennen will, durch $(\frac{D}{\Delta})^2$ beschränkt ist. Die SVM minimiert genau diesen Quotienten, da sie den Margin maximiert. Alternativ: Erklärung durch Strukturierung des Hypothesenraumes (TODO).
  • Reinforcement Learning
    • Wie lautet die Bellman-Gleichung?
      → $Q(s, a) = r + \gamma \max_{a'} Q(s', a')$ wobei $\gamma$ ein Diskontierungsfaktor ist, $s'$ der Zustand in den man kommt, wenn man $a$ ausführt und $r$ der Reward nach ausführen von $a$ in $s$ ist.
    • Was ist Value Iteration und wie lautet die Formel?
      → Schätzen der Value-Funktion durch iteratives anwenden von $\hat{V}^*(s_t) \leftarrow r_t + \gamma \hat{V}^*(s_{t+1})$
    • Was sind Eligibility Traces im Kontext von Reinforcement Learning?
      → Siehe oben
    • Wie funktioniert Q-Learning?
      → Siehe Abschnitt Q-Learning
  • Evolutionäre Algorithmen: Was ist wichtig?
    • Population / Individuen: Wie Individuen darstellen
      → Durch Gene (Attribute), z.B. als Bitstring
    • Gegebener Ablauf (Wahl der Eltern, Generierung der Individuen)
    • Wie kann man Kombinieren?
      → vgl. Rekombination
    • Fitness Function
    • Was sind die wichtigsten Elemente von evolutionären Algorithmen?
      → Mutation, Rekombination, Fittness-Funktion, Selektion
    • Was ist Landmarksche / Baldwinsche Evolution?
  • Wie lautet die Fehlerabschätzung von Vapnik?
    → Siehe Abschätzung des realen Fehlers durch den empirischen Fehler und die VC-Dimension.
  • Was versteht man unter Cascade Correlation?
    → YouTube (4:05 min)
  • Welche übwerwachten Lernverfahren gibt es?
    → Neuronale Netze, SVMs
  • Wie funktioniert Inferenz in Markov Logik Netzen?
    → Siehe oben
  • Wie wird die Verbundwahrscheinlichkeit / Weltwahrscheinlichkeit in Markov Logik Netzen berechnet?
    → Siehe oben
  • Was ist Dynamic Decay Adjustment (DDA)?
    → Siehe oben
  • Was ist erklärungsbasierte Generalisierung (EBG)?
    → Der Agent lernt keine neuen Konzepte, aber er lernt über Verbindungen bekannter Konzepte.
  • Wie lautet die Formel für Entropie / Information Gain?
    → $\text{Entropie} = - \sum_{i} p_i \log p_i$ und $KL(P, Q) = \sum_{x \in X} P(x) \cdot \log \frac{P(x)}{Q(x)}$
  • Was ist Cobweb?
    → Siehe Unsupervised Learning

Literatur

  • [Mit97] T. Mitchell. Machine Learning. McGraw-Hill, 1997.
  • [Dar09] A. Darwiche. Modeling and reasoning with Bayesian networks. Cambridge University Press, Cambridge [u.a.], 2009.
  • [Ber95] M. Berthold and J. Diamond. Boosting the Performance of RBF Networks with Dynamic Decay Adjustment. Advances in Neural Information Processing, 1995. [Online]
  • [Pro06] Prokopenko, Mikhail and Gerasimov, Vadim and Tanev, Ivan. Evolving Spatiotemporal Coordination in a Modular Robotic System. Springer, 2006.

Übungsbetrieb

Es gibt keine Übungsblätter, keine Übungen, keine Tutorien und keine Bonuspunkte.

Vorlesungsempfehlungen

Folgende Vorlesungen sind ähnlich:

Folgende Vorlesungen habe ich nicht gehört, könnten aber interessant sein:

Noch kann ich folgende Veranstaltungen nicht einschätzen und würde mich über Feedback von dir freuen:

Termine und Klausurablauf

Datum: Mündliche Prüfung (in Zukunft schriftlich)
Ort: nach Absprache
Zeit: 15 min
Übungsschein: gibt es nicht
Bonuspunkte: gibt es nicht
Ergebnisse: werden ca. 5 - 10 min. nach der mündlichen Prüfung gesagt
Erlaubte Hilfsmittel: keine

Published


by

Category

German posts

Tags

Contact