Neuronale Netze - Klausur

Dieser Artikel beschäftigt sich mit der Vorlesung „Neuronale Netze“ am KIT. Er dient als Prüfungsvorbereitung. Ich habe die Vorlesungen bei Herrn Prof. Dr. Alexander Waibel im Sommersemester 2015 gehört.

Behandelter Stoff

Vorlesung

Datum Kapitel Inhalt
15.04.2015 Einleitung -
21.04.2015 LVQ and related Techiques k-Means, OLVQ1, kompetitives Lernen, Mode Seeker, PCA
22.04.2015 - Übung
28.04.2015 Perceptron -
12.05.2015 Auto-Encoder Denoising- und Sparse Autoencoder, Bottleneck-Features, Kullback-Leibler-Divergenz; Kettenregel
13.05.2015 Deep Learning Momentum, Rprop, Newbob, L1/L2-Regularisierung ($|w|$, $w^2$), weight decay
19.05.2015 Übung -
20.05.2015 Übung -
26.05.2015 SOM Hebbian Learning, "VQ" mit SOM
09.06.2015 Effizientes Lernen Paralleles Lernen; Quickprop; Alternative Fehlerfunktion (cross entropy, CFM); weight elimination / regularization
15.07.2015 Summary When to use which objective function (cross entropy, MSE); Backpropagation; Weight initialization; Regularization (L2 weight decay, dropout); Time Delay NN; Recurrent Networks; Applications (Speech Recognition, Computer Vision)

NN01-Intro.pdf

  • Human Brain vs. Computer (Processing/Processors, Accuracy, Speed, Hardware, Design)
  • Aufbau eines biologischen Neurons (vgl. Wikipedia)

NN02-Classification.pdf

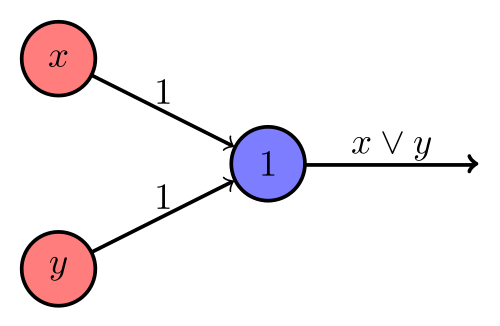
Rosenblatt-Perceptron which realizes logical or
Rosenblatt-Perceptron which realizes logical or
  • McCulloch-Pitts Neuron (weights, bias, activation function is step function)
  • Rosenblatt Perceptron Algorithmus
  • Backpropagation
  • Curse of Dimensionality
  • Parzen Window
  • Features: Nominal, Ordinal, Intervallskaliert, Verhältnisskaliert
Bayes-Rule
Given events $A_1$, $A_2$ and $B$, Bayes' rule states that the conditional odds of $A_1:A_2$ given $B$ are equal to the marginal odds of $A_1:A_2$ multiplied by the Bayes factor or likelihood ratio $\Lambda$: $$O(A_1:A_2|B) = \Lambda(A_1:A_2|B) \cdot O(A_1:A_2) ,$$ where $$\Lambda(A_1:A_2|B) = \frac{P(B|A_1)}{P(B|A_2)}.$$
Parametrischer Klassifizierer
Ein Klassifizierer heißt parametrisch, wenn er eine Wahrscheinlichkeitsverteilungsannahme macht.
Naiver Bayes-Klassifikator
Ein Klassifizierer heißt naiver Bayes-Klassifikator, wenn er den Satz von Bayes unter der naiven Annahme der Unabhängigkeit der Features benutzt.
Normalverteilung
Eine stetige Zufallsvariable $X$ mit der Wahrscheinlichkeitsdichte $f\colon\mathbb{R}\to\mathbb{R}$, gegeben durch
$f(x) = \frac {1}{\sigma\sqrt{2\pi}} e^{-\frac {1}{2} \left(\frac{x-\mu}{\sigma}\right)^2}$
heißt $\mathcal N\left(\mu, \sigma^2\right)$-verteilt, normalverteilt mit den Erwartungswert $\mu$ und Varianz $\sigma^2$.
Multivariate Normalverteilung
Eine $p$-dimensionale reelle Zufallsvariable $X$ ist normalverteilt mit Erwartungswertvektor $\mu$ und (positiv definiter) Kovarianzmatrix $\Sigma$, wenn sie eine Dichtefunktion der Form $$f_X(x)=\frac{1}{ \sqrt{(2\pi)^p \det(\Sigma)} } \exp \left( -\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu) \right)$$ besitzt. Man schreibt $$X\sim \mathcal N_p(\mu, \Sigma).$$
Gauß'scher Klassifizierer
Ein (naiver) Bayes-Klassifikator, welcher von normalverteilten Daten ausgeht heißt Gauß'scher Klassifizierer.
Principal Component Analysis (PCA, Hauptkomponentenanalyse)
Die Hauptkomponentenanalyse ist ein Verfahren zur Dimensionalitätsreduktion von ungelabelten Daten im $\mathbb{R}^n$. Sie projeziert die Daten auf diejenige Hyperebene im $\mathbb{R}^d$, die den durch die Projektion stattfindenden Datenverlust minimal hält. Dabei ist $d \in 1, \dots, n$ beliebig wählbar. Die Transformation der Daten $X$ findet durch eine Matrixmultiplikation $Y = P \cdot X$ statt. Die Matrix $P$ besteht aus den ersten $d$ Eigenvektoren der Kovarianzmatrix der Features $X$: $P = (v_1, \dots, v_d)$ mit $\lambda_j v_j = C_X v_j$ für $j=1,\dots,d$ Außerdem gilt: $C_X = \frac{1}{n-1} X X^T$

V03: LVQ

Slide name: V03_2015-04-21_LVQ.pdf

  • k-Means
  • Fuzzy k-Means
  • Vector Quantization (VQ) is an unsupervised clustering algorithm
  • Learning Vector Quantization is supervised.

V04: Perceptron

Slide name: V04_2015-04-28_Perceptron.pdf

McCulloch–Pitts (MCP) Neuron
Ein MLP-Neuron is ein Algorithmus zur binären Klassifizierung. Er hat $m+1$, mit $m \in \mathbb{N}_{> 0}$ inputs $x_i \in \{0, 1\}$. Davon ist der erste (nullte) Konstant gleich Eins und wird Bias genannt. Jeder Input wird mit eingem Gewicht $w_i \in \mathbb{R}$ multipliziert, alle gewichteten Inputs werden addiert und schließlich wird die Stufenfunktion $\varphi(x) = \begin{cases}1 &\text{falls } x > 0\\0 &\text{sonst} \end{cases}$ angewendet. Man lernt mit MCP Neuronen, indem man $$\Delta w = \eta \delta x$$ $$w \gets w + \Delta w$$ berechnet, wobei $\eta \in (0, 1)$ die Lernrate ist, $x$ ein Trainingsdatum und $\delta = y_{\text{target}} - y$ die Abweichung vom gewünschten Ergebnis ist. Diese Regel wird auch Perceptron Learning Rule genannt.
Rosenblatt-Perzeptron
Wie das McCulloch–Pitts (MCP) Neuron, nur ist $x_i \in \mathbb{R}$ und ein Lernalgorithmus ist gegeben. Dieser addiert den $\eta \in (0, 1)$ gewichteten, fehlklassifizierten Vektor auf die Gewichte $w_i$. $\eta$ heißt die Lernrate. Man lernt mit MCP Neuronen, indem man $$\Delta w = \eta \delta x$$ $$w \gets w + \Delta w$$ berechnet, wobei $\eta \in (0, 1)$ die Lernrate ist, $x$ ein Trainingsdatum und $\delta = - \frac{\partial E}{\partial w}$ der Gradient auf der Fehleroberfläche in Abhängigkeit von den Gewichten ist. Es wird also Gradient descent verwendet.
Pocket Perceptron Algorithm
Ein Lernalgorithmus für ein Rosenblatt-Perzeptron. Dieser konvergiert zu Gewichten, welche die wenigsten Beispiele falsch klassifiziert.
Sigmoid-Funktion
$\varphi(x) = \frac{1}{1+e^{-x}}$
Softmax-Funktion
$\varphi(a_i) = \frac{e^{a_i}}{\sum_{k} e^{a_k}}$ wobei $a_i$ die Aktivierung des $i$-ten Neurons der selben Schicht ist.
Perzeptron / Logistic Neuron
MSE + Sigmoid activation function

Fakten:

  • Das Rosenblatt-Perzeptron findet eine lineare Trenngrenze, wenn sie existiert.
  • Probleme vom Rosenblatt-Perzeptron:
  • Nicht-linear trennbare Daten wie z.B. das XOR-Problem
  • Nicht-trennbare Daten
  • Wahl der Lernrate und der Startgewichte
  • Aufbau eines biologischen Neurons (Axon, Dendriten, Zellkörper, Ranviersche Schnürringe, Synapsen)
  • Glia-Zellen

V05: Features

Slide name: V05_2015-04-29_Features.pdf

Rectified Linear Unit (ReLU)
$\varphi(x) = \max(0, x)$
Leaky ReLU
$\varphi(x) = \max(0.01x, x)$
Softplus
$\varphi(x) = \log(1 + e^x)$
Feed Forward Neural Network
A Feed Forward Neural Network is a learning algorithm which takes a fixed-size input feature vector, applies varous matrix multiplications and point-wise non-linear functions to obtain a fixed-size output vector.
Multilayer Perceptron
A Multilayer Perceptron is a special type of Feed Forward Neural Network. It consists of fully connected layers only.
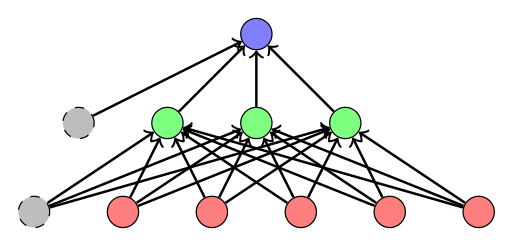
Draft of a multilayer Perceptron (MLP).
Figure 1: Draft of multilayer Perceptron (MLP). The bias units are grey, the input units are red, the hidden units are green and the output unit is blue. The edges are directed from input, to hidden, to output and from the bias to hidden / output.
Metrik
Sei $X$ eine Menge und $d:X \times X \rightarrow \mathbb{R}$ eine Abbildung. $d$ heißt Metrik auf $X$, wenn gilt:
  • $d(x, y) = 0 \geq x=y \;\;\; \forall x, y \in X$
  • $d(x,y)=d(y,x)$
  • $d(x,y) \leq d(x,z) + d(z,y)$
Jaccard-Metrik
Es seien $A, B$ Mengen und $J(A, B) := \frac{|A \cup B| - |A \cap B|}{|A \cup B|}$. Dann heißt $J$ die Jaccard-Metrik.
Levenshtein-Distanz
Es seien $a, b$ Zeichenketten, $|a|$ die Länge der Zeichenkette $a$ und $\delta_{a_i \neq b_j}$ genau dann 1, wenn das $i$-te Zeichen von $a$ und das $j$-te Zeichen von $b$ sich unterscheiden. Dann heißt $d_L(a, b)$ die Levenshtein-Distanz: $$d_L(a,b) := lev_{a,b}(|a|, |b|)$$ $$\text{lev}_{a,b}(i, j) = \begin{cases}\max(i,j) &\text{falls} \min(i,j) = 0,\\ \min \begin{cases}\text{lev}_{a,b}(i-1,j)+1\\ \text{lev}_{a,b}(i,j-1)+1\\ \text{lev}_{a,b}(i-1,j-1)+\delta_{(a_i \neq b_j)}\\\end{cases} &\text{sonst}\end{cases}$$

Fragen:

  • Welche Feed Forward Neuronalen Netze existieren, die keine Multilayer Perceptronen sind?
    → CNNs, TDNNs, SOMs.
  • Welche Skalentypen gibt es für Merkmale (Features)?
    • Nominale Merkmale: Nur Gleichheit kann überprüft werden
    • Ordinale Merkmale: Es existiert eine "kleiner gleich"-Relation
    • Intervallskalierte Merkmale:
      • Die Differenz der Merkmale hat eine Semantik
      • Es existiert jedoch kein "wirklicher" Nullpunkt
    • Verhältnisskalierte Merkmale: Wie Intervallskaliert, aber mit absolutem Nullpunkt.

V06: Backpropagation

Slide name: V06_2015-05-05_Backpropagation.pdf

Kreuzentropie Fehlerfunktion (Cross-Entropy)
$$E_{-x} = - \sum_{k}[t_k^x \log(o_k^x) + (1-t_k^x) \log (1- o_k^x)]$$ wobei $x$ der Feature-Vektor ist, $k$ ein Neuron des letzen Layers, $t$ der wahre Wert (d.h. der gewünschte Output), $o$ der tatsächliche Output ist.
  • Stochastic Gradient Descent
  • Batch Gradient Descent

V07: Feature Learning

Slide name: V07_12-05-2015_Feature_Learning.pdf

Autoencoder
Ein Autoencoder ist ein neuronales Netz, welches darauf trainiert wird die Input-Daten am Output wieder zu replizieren.
Bottleneck Features
Unter Bottleneck-Features versteht man eine Schicht in einem neuronalem Netz, welche wesentlich kleiner ist als die vorhergehende und nachfolgende Schicht.
Kullback-Leibler-Divergenz
Die Kullback-Leibler-Divergenz ist ein Maß für die Unterschiedlichkeit zweier Wahrscheinlichkeitsverteilungen $P, Q$. Für diskrete Verteilungen ist sie definiert als: $$KL(P||Q) := \sum_{x \in X} P(x) \cdot \log \frac{P(x)}{Q(x)}$$
Denoising Autoencoder
Ein Autoencoder, welcher trainiert wird rauschen zu entfernen.

Fakten:

  • Eine lineare Aktivierungsfunktion wird in einer Repräsentation im Bottleneck-Feature resultieren, die PCA ähnelt.
  • Fehlerfunktion:
  • CE bei binären Ausgaben (d.h. Input-Features)
  • MSE bei reelen Ausgaben (d.h. Input-Features)

Fragen:

  • Wie muss man die Grafik zu Stacked Denoising Autoencodern verstehen?

V08: Deep Learning

Slide name: V08_2015-05-13_Deep_Learning.pdf

Deep Neural Networks
Neural Networks with at least two hidden layers with nonlinear activation functions.
Hyperparameter
Hyperparameter $\theta$ eines neuronalen Netzes sind Parameter, welche nicht gelernt werden.
Learning Rate Scheduling
Start with a learning rate $\eta$ and reduce it while training.
Exponential Decay Learning Rate
$\eta_t = \eta_{t-1} \cdot \alpha = \eta_0 \cdot \alpha^t$ mit $\alpha \in (0, 1)$
Performance Scheduling
Measure the error on the cross validation set and decrease the learning rate when the algorithm stops improving.
RProp
RProp is a learning rate scheduling method which is only based on the sign of the gradient. It increases the learning rate when the sign of the gradient doesn't change and decreases or resets it when the sign of the gradient changes. Rprop has an own learning rate for every single feature.
AdaGrad (vgl. Folie 34)
$$\eta_{tij} = \frac{\eta_0}{\sqrt{1 + \sum_k {(\frac{\partial E^{t-k}}{\partial w_{ij}})}^2}}$$ where $\eta_0$ is an initial learning rate, $t$ is the epoch, $i,j$ refer to neurons.
Newbob Scheduling
Newbob scheduling is a combination of exponential decay learning rate scheduling and performance scheduling. It starts with a learning rate $\eta_0$. When the validation error stops decreasing, switch to exponentially decaying learning rate. Terminate when the validation error stops decreasing again.
Cross Entropy Error function (CE)
$$E_{CE}(w) = - \sum_{x \in X} \sum_{k} [t_k^x \log(o_k^x) + (1-t_k^x) \log(1-o_k^x)]$$ where $w$ is the weight vector, $X$ is the set of training examples (feature vectors), $t_k^x = \begin{cases}1 &\text{if } x \text{ is of class }k\\0&\text{otherwise}\end{cases}$ and $o_k^x$ is the output at neuron $k$ of the network for the feature vector $x$.
Mean Squared Error function (MSE)
$$E_{MSE}(w) = \frac{1}{2}\sum_{x \in X} \sum_{k} (t_k^x - o_k^x)^2$$ where $w$ is the weight vector, $X$ is the set of training examples (feature vectors), $k$ is the range of output neurons, $t_k^x = \begin{cases}1 &\text{if } x \text{ is of class }k\\0&\text{otherwise}\end{cases}$ and $o_k^x$ is the output at neuron $k$ of the network for the feature vector $x$.
Convolutional Neural Networks (CNNs)
Feed-Forward Neuronale Netze, welche durch geteilte Gewichte (weight sharing) grafische Filter lernen. CNNs sind aktuell in der Computer Vission Stand der Technik.
Time-Delay Neural Networks (TDNNs)
TDNNs wenden wie CNNs weight sharing an um Filter zu lernen. Sie werden in der ASR verwendet und lernen auch Filter. Allerdings wird hier über die Zeit hinweg gefaltet.
Multi-State Time-Delay Neural Networks (MS-TDNNs, siehe [Haf92])
MS-TDNNs codieren die alignment-Suche im Netzwerk. Sie sind hybride Netze (so wie HMM-DeepNN Hybrids von Mircosoft).
RProp by Ryan Harris
RProp by Ryan Harris (source). Rot ist der Gradientenabstieg, blau ist mit momentum, rosa ist RProp
  • Pretraining
  • Design choices (hyperparameters):
    • Topology (Width of layers, number of layers)
    • Activation functions
    • Error function
    • Mini-Batch size
    • Training function
    • Preprocessing
    • Initial Weights
  • MSE vs CE:
    • MSE penetalizes large differences much more than small ones
    • MSE works well for function approximation
    • CE works well on classification tasks

V09: Reinforcement Learning

Slide name: V09_2015-05-26-Reinforcement-Learning.pdf

Markov Decision Process (MDP)
Siehe ML 1.
Diskontierungsfaktor
Siehe Probabilistische Planung.
Strategie (engl. Policy)
Siehe Probabilistische Planung.
Q-Funktion (Action-Value function)
Siehe Probabilistische Planung.
V-Funktion (State-Value function)
Siehe ML 1.
$\varepsilon$-Greedy Strategy
Siehe Probabilistische Planung.
$\varepsilon$-decreasing Strategy
Siehe Probabilistische Planung.
$\varepsilon$-first Strategy
Siehe Probabilistische Planung.
Adaptive $\varepsilon$-greedy Strategy
Siehe Probabilistische Planung.
Episode
Siehe Probabilistische Planung.
Monte Carlo Policy Evaluation
Initialize state values $V^\pi$ and iterate:
  1. Generate an episode
  2. foreach state $s$ in episode:
    1. Get the reward $\hat{R}$ from that state on
    2. $\hat{R} = \sum_{j=0}^\infty \gamma^j r_j$
    3. $V_{k+1}^\pi (s) \leftarrow V_k^pi (s) (1-\alpha)+\alpha \hat{R}$
where $\alpha$ is the learning rate.
Temporal Difference Learning (TD-Learning)
Siehe ML1
Q-Learning
Siehe Probabilistische Planung.
SARSA
Siehe Probabilistische Planung.
Strategie-Iteration (Policy iteration)
Siehe Probabilistische Planung.

Konvention:

  • Eine optimale Strategie wird mit \(\pi^*\) bezeichnet.

Fragen:

  • Was bedeutet es, wenn in einem MDP der Diskontierungsfaktor \(\gamma = 0\) ist?
    → Nur der aktuelle Reward ist wichtig. Effektiv nimmt der Agent immer das nächste Feld, welche den höchsten Reward bietet (bzw. die Aktion, die den größten 1-Aktion Erwartungswert liefert).
  • Was bedeutet es, wenn in einem MDP der Diskontierungsfaktor \(\gamma = 1\) ist?
    → Der Agent versucht die Summe der Belohnungen insgesamt zu maximieren.

Siehe auch:

V10: SOM

Slide name: V10_2015-05-26_SOM.pdf

Hebbsche Lernregel
what fires together, wires together
Selbstorganisierende Karten (SOM, Kohonennetze)
SOMs sind eine Art von Neuronalen Netzen. Die neuronen von SOMs sind auf einem Gitter angeordnet. Es gibt nur zwei Schichten: Die Input-Neuronen und die Neuronen auf dem Gitter. Jedes Input-Neuron ist mit jedem Neuron auf dem Gitter verbunden.
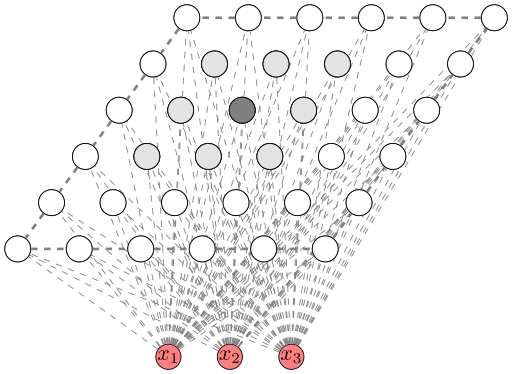
Draft of a self-organizing map (SOM).
Figure 2: Draft of self-organizing map (SOM).
Training:
  1. Initialisierung: Die Gewichte $w_{ji}$ von dem $i$-ten Input-Neuron zum Neuron ($i = 1, ..., n$) $j$ auf dem Gitter werden zufällig initialisiert.
  2. Sampling: Nehme ein zufälliges Beispiel $x$ der Trainingsdaten.
  3. Matching: Finde das Neuron $j_{\text{min}}$, für das die Gewichte dem Input am ähnlichsten sind:
    $$j_{\text{min}} = \text{arg min}_j \sum_{i=1}^n (x_i - w_{ji})^2$$
  4. Update: Passe die Gewichte des gewinnenden Neurons $i$ sowie der Nachbarschaft $j$ an: $w_j = w_j + \eta h(j, i(x))(x - w)$
  5. Repeat: Und zurück zu Schritt 2.
Siehe auch:

V11: RBMs

Slide name: V11_2015-05-27_RBMs

Hopfield-Netz (siehe [Hop82], [Kri05])
Ein Hopfield-Netz besteht nur aus einer Schicht von McCulloch-Pitts Neuronen. Jedes Neuron ist mit jedem anderen Neuron (also nicht sich selbst) und allen Inputs verbunden. Die Schicht funktioniert gleichzeitig als Ein- und Ausgabeschicht. Hopfield-Netze werden in einem einzigen durchgang Trainiert. Dabei wird auf das Gewicht von Neuron $i$ zu Neuron $j$ + 1 addiert, wenn das Bit $i$ des Trainingsmusters gleich ist. Falls das nicht der Fall ist, wird von dem Gewicht 1 subtrahiert: $$w_{ij} = \sum_{p} (2 a^{(i)}_p - 1) \cdot (2 a^{(j)}_p - 1)$$ Jedes Gewicht ist zum start des Trainings 0. Das Training ist also einfach nur ein Zählen, wie häufig die Stellen übereinstimmen.
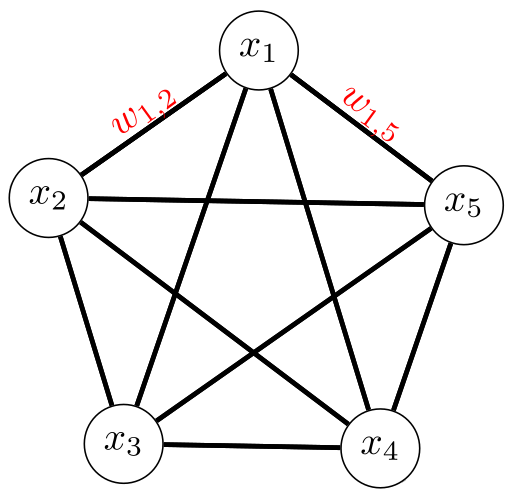
Draft of a hopfield network.
Figure 3: Draft of Hopfield network. Every node is an input node. The McCullogh-Pitts nodes are updated asynchronously. When the state of the node doesn't change any more, they contain the output of the network. Learned are the weights between the nodes.
Boltzmann-Maschine
Boltzmann-Maschinen sind stochastische neuronale Netzwerke, welche duch belibige ungerichtete Graphen repräsentiert werden können. Die neuronen sind binär; sie feuern also entweder oder nicht. Es gibt insbesondere keine Unterschiede in der Stärke mit der sie feuern. Siehe auch: Scholarpedia
Restricted Boltzmann machine (RBM)
Eine RBM ist ein neuronales Netz mit nur einem Hidden Layer. Es ist gleichzeitig ein Spezialfall von MRFs. Im Gegensatz zur Boltzmann-Maschine muss die Restricted Boltzmann-Machine (RBM) aus einem bipartitem Graph bestehen. Dies erlaubt ein effizienteres Trainingsverfahren (Contrastive Divergence). Die Energie des Netzwerkes ist $$- \sum_{i < j} w_{ij} s_i s_j - \sum_i b_i s_i$$ wobei $s_i, s_j$ die binären Zustände der Knoten $i, j$ sind. Der Name "Boltzmann" kommt von dieser Energie (man kann den Netzwerkzuständen wahrscheinlichkeiten zuweisen, die direkt Proportional zu $e^{-E}$) sind.
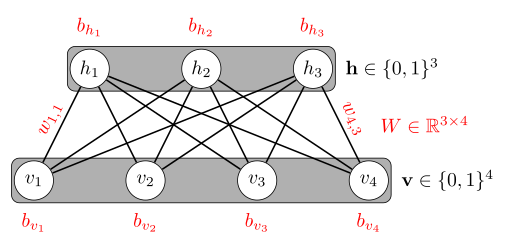
Draft of an RBM.
Figure 4: Draft of an RBM. The learned parameters are red.
Es werden keine Verbindungen zwischen den Hidden Units erlaubt (daher das "restricted" - Quelle: Hinton, 2015).

Siehe A Practical Guide to Training Restricted Boltzmann Machines von Hinton, 2010.
sowie Interence in RBMs
Contrastive Divergence (CD, CD-$k$, siehe YouTube Video, 2 von Hugo Larochelle)
Contrastive Divergence ist ein Trainingsalgorithmus für RBMs. Ein Hyperparameter ist $k \in \mathbb{N}$. Er geht wie folgt vor:
  1. Lege den Trainingsvektor $x^{(t)}$ an die Eingabeknoten an.
  2. Berechne die Wahrscheinlichkeit für jede Hidden Unit, dass diese gleich 1 ist. Setze sie mit dieser Wahrscheinlichkeit gleich 1.
  3. Berechne die Wahrscheinlichkeit für jeden Eingabeknoten, dass dieser gleich 1 ist. Setze ihn mit dieser Wahrscheinlichkeit gleich 1.
  4. Gehe zu Schritt 2. Wiederhole dies für $k$ Schritte (dies wird auch Gibbs-Sampling genannt). Das, was nach dem $k$-fachem Gibbs-Sampling in der Eingabeschicht steht wird auch "negative sample $\tilde x$" genannt.
  5. Update der Parameter: \begin{align} W &\leftarrow W + \eta (h(x^{(t)}) {x^{(t)}}^T - h(\tilde x) {\tilde x}^T)\\ b_h &\leftarrow b_h + \eta (h(x^{(t)}) - h(\tilde x))\\ b_v &\leftarrow b_v + \eta (x^{(t)} - \tilde x) \end{align} wobei $\eta \in (0, 1) $ die Lernrate ist, $b_h \in \mathbb{R}^n_h$ der Bias-Vektor der Hidden Units und $b_v \in \mathbb{R}^{n_v}$ der Bias-Vektor der Eingabeknoten ist. $h = \text{sigmoid}(b_h + W x)$ ist ein Vektor, welcher für die einzelnen Hidden Units sagt wie wahrscheinlich es ist, dass diese gleich 1 sind.
In der Praxis funktioniert es schon mit $k=1$ für Pre-Training. Wenn $k$ groß ist konvergiert $\tilde x$ gegen den wahren Modellwert. Das wäre dann eine Monte-Carlo Estimation.
Simulated annealing
Simulated annealing ist ein heuristisches Optimierungsverfahren. Sei $D$ ein Wertebereich einer Funktion $f: D \rightarrow \mathbb{R}$ und $U: D \rightarrow \mathcal{P}(D)$ eine Funktion, welche die Umgebung eines Punktes angibt. Sei $T: \mathbb{N}_0 \rightarrow \mathbb{R}_{> 0}$ die Temperatur zum Zeitpunkt $t \in \mathbb{N}_0$. Gesucht ist $\text{arg min}_{x \in D} f(x)$. Wähle zum Zeitpunkt $t=0$ einen zufälligen Startwert $x \in D$. Gehe nun iterativ vor und jeweils einen Zeitschritt weiter: Nehme einen Punkt aus der Umgebung $y \in U(x)$. Wenn $f(y) \leq f(x)$, dann überschreibe $x \leftarrow y$. Falls nicht, dann überschreibe es mit der Wahrscheinlichkeit $\exp \left (-\frac{f(y)-f(x)}{T(t)} \right )$. Speichere in jedem Schritt den bisher besten Wert.

Anwendungen:

  • Hopfield-Netze: Hopfield-Netze kann man für das TSP einsetzen und auch als Assoziativspeicher nutzen. Allerdings haben sich Hopfield-Netze nie wirklich durchgesetzt.
  • RBMs: Collaborative Filtering

Siehe auch:

V12: RNNs

Slide name: V12_2015-06-02_RNNs.pdf

Elman-Netz
Ein rekurrentes neuronales Netzwerk, bei dem die Ausgabe eines hidden layers im nächsten Zeitschritt als Eingabe verwendet wird.
Jordan-Netz
Ein rekurrentes neuronales Netzwerk, bei dem die Ausgabe der Ausgabeschicht im nächsten Zeitschritt als Eingabe verwendet wird.
Backpropagation through Time (BPTT)
Ein Trainingsalgorithmus für rekurrente neuronale Netze, bei dem das Netz "ausgerollt" wird. Das rekurrente Netz wird also als unendlich großes nicht-rekurrentes Netz behandelt.
Vanishing gradient problem
Das Problem des verschwindenden Gradienten ist eine Herausforderung im Kontext neuronaler Netze, welche mit Backpropagation trainiert werden. Insbesondere bei sehr tiefen oder rekurrenten Netzen kann es passieren, dass der Gradient bei den ersten Schichten sehr niedrig ist, sodass das Netz sehr langsam lernt. Aufgrund numerischer Ungenauigkeit kann dies sogar dazu führen, dass das Netz in den ersten Schichten nicht lernen kann.
Long short-term memory (LSTM)
Ein LSTM ist ein Typ eines neuronalen Netzwerks. Das besondere an LSTM Netzen sind "intelligente" Neuronen, welche über Gates bestimmen ob ein Wert gespeichert wird und wie lange.

Siehe auch:

V13: NN learning tricks

Slide name: V13_2015-06-09_NNlearning-tricks.pdf

Momentum
In der Update-Regel $\Delta w_{ij}^* (t+1) = \Delta w_{ij} (t+1) + \alpha \Delta w_{ij}(t)$ wird der Term $\Delta w_{ij}(t)$ als Momentum bezeichnet. Der Skalar $\alpha \in [0, 1]$ gewichtet diesen und ist ein Hyperparameter.

Siehe auch: Optimization: Stochastic Gradient Descent
Quickprop
Quickprop ist ein Trainingsverfahren für neuronale Netze. Der Lernalgorithmus nimmt an, dass die Fehlerebene lokal durch eine parabel approximiert werden kann. Das Gewichtsupdate im Schritt $k$ ist demnach vom Gradienten und dem Gewichtsupdate das vorherigen Schrittes abhängig: $$\Delta^{(k)} \, w_{ij} = \Delta^{(k-1)} \, w_{ij} \left ( \frac{\nabla_{ij} \, E^{(k)}}{\nabla_{ij} \, E^{(k-1)} - \nabla_{ij} \, E^{(k)}} \right)$$
Weight Decay
Passe die Fehlerfunktion an: $E = MSE + \lambda \sum_{i,j} w_{ij}^2$
Weight Elimination
Passe die Fehlerfunktion an: $E = MSE + \lambda \sum_{i,j} \frac{w_{ij}^2}{1+w_{ij}^2}$
Optimal Brain Damage (OBD)
Optimal Brain Damage entfernt nach dem Training Verbindungen die sehr kleine $|w_{ij}|$ haben. Besser: Entferne Verbindungen, die geringen Einfluss auf die Fehlerfunktion haben.
Cascade Correlation (siehe Fahlman und Lebiere: The Cascade-Correlation Learning Architecture)
Cascade Correlation ist ein konstruktiver Algorithmus zum erzeugen von Feed-Forward Neuronalen Netzen. Diese haben eine andere Architektur als typische multilayer Perceptrons. Bei Netzen, welche durch Cascade Correlation aufgebaut werden, ist jede Hidden Unit mit den Input-Neuronen verbunden, mit den Output-Neuronen und mit allen Hidden Units in der Schicht zuvor.


Siehe How exactly does adding a new unit work in Cascade Correlation?
Meiosis Netzwerke (siehe Stephen Jose Hanson: Meiosis Networks)
Meiosis Netzwerke bauen ein neuronales Netz auf. Sie beginnen mit einer einzelnen hidden Unit. Diese hidden Unit wird aufgespalten, wenn die "Unsicherheit" zu groß ist (vgl. paper für Kritierum; vgl. summary).
Automatic Structure Optimization (ASO, siehe [Bod93])
Der ASO-Algorithmus passt folgende Hyperparameter im Training automatisch an:
  • Anzahl der Hidden Units
  • Größe des Input-Fensers (ASR-Spezifisch)
  • Anzahl der Zustände, welche "Accoustic Events" repräsentieren
Classification Figure of Merit (CFM, siehe [Ham90])
$$E_{CFM}(w) = \sum_k \frac{\alpha}{1 + e^{-\beta \Delta_k + \gamma}}$$ wobei
  • $k$: Klasse
  • $\alpha, \beta, \gamma$: Hyperparameter
  • $\Delta_k = o_t - o_k$: Differenz des wahren (true) nodes und des anderen Knotens.

Speed-ups des Trainings sind möglich durch:

  • Momentum
  • Überspringen von bereits gut gelernten Beispielen
  • Dynamische Anpassung der Lernrate \(\eta\)
  • Quickprop
  • Gute Initialisierung (z.b. \(w \sim U(- 4 \cdot \sqrt{\frac{6}{n_j + n_{j+1}}}, 4 \cdot \sqrt{\frac{6}{n_j + n_{j+1}}})\))

Lernen kann getweakt werden:

  • Den Betrag des Gradienten um eine kleine Konstante vergrößern (Folie 19+20)
  • Fehlerfunktion anpassen
  • Overfitting verhindern
    • Weight decay
    • Weight elimination
    • Optimal Brain Damage
    • Optimal Brain Surgeon
  • Schrittweise Netzkonstruktion
    • Cascade Correlation
    • Meiosis Netzwerke
    • ASO

V14: DNN CV

Slide name: V14_2015-06-10_DNN_CV .pdf

SIFT (Scale-invariant feature transform)
Unter SIFT versteht man bestimmte Features in der Bildverarbeitung, welche invariant unter skalierung sind.
Texton (siehe UCLA)
Unter einem Texton versteht man grundlegende, kleine Features eines Bildes. Diese Bilden die kleinsten als unterschiedlich wahrnehmbaren Einheiten.
Convolutional Neural Network (CNN)
Ein CNN ist ein Neuronales Netzwerk, welches mindestens eine Schicht hat, welche die Parameter eines Kernels für eine Faltung lernt.
Feature Map
Im Kontext von CNNs versteht man unter einer Feature-Map die Ausgabe eines Kernels in einem Convolutional Layer.

Facts:

  • Pooling: Max, Mean, Probabilistic

V15: Speech-Independence

Slide name: V15_2015-06-17_Speech-Independence.pdf

Visualisierung von Netzen

Häufig wird die Architektur neuronaler Netze grafisch dargestellt. Dabei ist mir folgendes aufgefallen:

  • Im Innenren von Neuronen wird die Aktivierungsfunktion "geplottet". Das heißt bei der Sigmoidfunktion wird etwas S-Förmiges dargestellt, bei der sign-Funktion etwas eckiges, bei ReLU ein horizontaler Strich gefolgt von einem Strich im 45-Grad Winkel.
  • Typischerweise ist der Input links (oder alternativ unten) und der Output rechts (oder alternativ oben)

Interpretation of errors

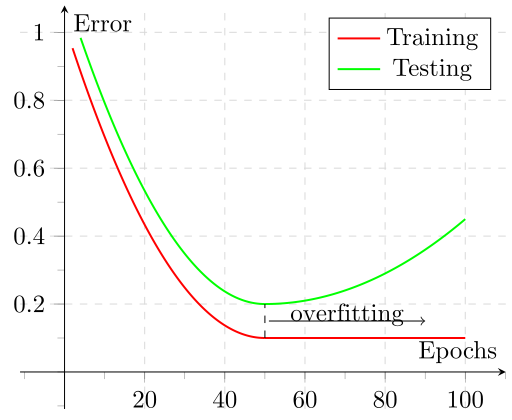
Training and Testing error over epochs
Figure 5: Training and Testing error over epochs. At some point overfitting happens.
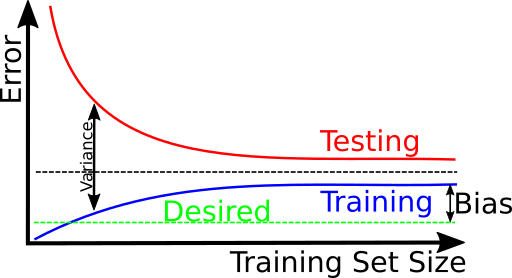
Training and Testing error over training data
Figure 6: Training and Testing error over training data. At some point overfitting happens.

If you have a problem with high variance, you can train more epochs, get more data or better features.

If you have a problem with high bias, you should get better features or a better classifier.

Please note that Figure 6 also gives you a feeling for how much new training data will help you with your problem.

Aktivierungsfunktionen

Name Function $\varphi(x)$ Range of values Differentiable $\varphi'(x)$ Layer Comment
Signum $\varphi(x) = \begin{cases}+1 &\text{if } x > 0\\-1 &\text{if } x < 0\end{cases}$ $\{-1, 1\}$ Yes
(except 0)		 $\varphi'(x) = 0$ No  
Heaviside Step function $\varphi(x) = \begin{cases}+1 &\text{if } x > 0\\0 &\text{if } x < 0\end{cases}$ $\{0, 1\}$ Yes
(except 0)		 $\varphi'(x) = 0$ No McCullch-Pitts; Rosenblatt
Sigmoid $\varphi(x) = \frac{1}{1+e^{-x}}$ $[0, 1]$ Yes $\varphi'(x) = \frac{e^x}{(e^x +1)^2}$ No Smoothed version of the heaviside step function
tanh $\varphi(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \tanh(x)$ $[-1, 1]$ Yes $\varphi'(x) = \text{sech}^2(x)$ No Smoothed version of the signum function
ReLU $\varphi(x) = \max(0, x)$ $[0, \infty)$ Yes
(except 0)		 $\varphi'(x) = \begin{cases}1 &\text{if } x > 0\\0 &\text{if } x < 0\end{cases}$ No Standard in CNNs
Leaky ReLU $\varphi(x) = \max(\alpha x, x)$ mit typischerweise $\alpha = 0.01$ $(-\infty, +\infty)$ Yes
(except 0)		 $\varphi'(x) = \begin{cases}1 &\text{if } x > 0\\0.01 &\text{if } x < 0\end{cases}$ No Fixes the dying ReLU problem[1]
Softplus $\varphi(x) = \log(e^x + 1)$ $(0, \infty)$ Yes $\varphi'(x) = \frac{e^x}{e^x + 1}$ No Smoothed ReLU
ELU $\varphi(\mathbf{x}) = \begin{cases}x &\text{if } x > 0\\\alpha (e^x - 1) &\text{otherwise}\end{cases}$ $(-\infty, +\infty)$ Yes $\varphi'(x) = \begin{cases}1 &\text{if } x > 0\\\alpha e^x &\text{otherwise}\end{cases}$ No  
Softmax $o(\mathbf{z})_j = \frac{e^{z_j}}{\sum_{k=1}^K e^{z_k}}$ $[0, 1]^K$ Yes differentiable Yes Standard for classification problems as the output can be interpreted as a probability distribution.
Maxout $o(\mathbf{z}) = \max_{z \in \mathbf{z}} z$ $(-\infty, +\infty)$ No - Yes  

See also:

Topology Learning

Growing approaches

Pruning approaches

Genetic Approaches

See also:

Einordnung

Neuronale netze kann man durch folgende Kriterien mit einander vergleichen:

  • Deterministisch / Stochastisch: Ist die Aktivierung der neuronen stochastische oder deterministisch?
  • Inferenz: Feed-Forward oder Rekurrent? Wie funktioniert die Auswertung?
  • Training: Wie lernt man?
  • Verwendung: Wo wird das Netzwerk typischerweise eingesetzt?
Netzwerk Deterministisch Inferenz Training Verwendung
McCulloch-Pitts Neuron Yes Feed-Forward Supervised Classification of linear separable data
Rosenblatt Perceptron Yes Feed-Forward Supervised Classification of linear separable data
Multilayer Perceptron Yes Feed-Forward Supervised (Backpropagation) Classification
CNN Yes Feed-Forward Supervised (Backpropagation + weight sharing) Computer Vision
TDNNs Yes Feed-Forward Supervised (Backpropagation + weight sharing) ASR
LSTM Yes Recurrent BPTT Mapping sequences (Generating texts, machine translation)
SOMs Yes Feed-Forward Unsupervised (competitive learning) Visualisierung / Dimensionalitätsreduktion: Mapping of high-dimensional data on 2D; CBIR; TSP
Hopfield networks Yes Recurrent Unsupervised (Hebbsche Lernregel) Associative memories, travelling salesman
Boltzmann machines stochastic Simulated Annealing Annealed Importance Sampling (not used)
RBMs stochastic $p(h_j=1|x) = \text{sigmoid}(b_{v,j} + W_j x)$
$p(x_k=1|h) = \text{sigmoid}(b_{h,k} + h^T W_k)$		 Contrastive Divergence (CD-$k$) Collaborative Filtering

Learning Rate Scheduling

There are a couple of publications which deal with LR scheduling:

I'm not too sure, but I think momentum is not a learning rate scheduling algorithm.

See also:

Prüfungsfragen

  • Was ist der Unterschied zwischen Backpropagation und Gradient descent?
    → Backpropagation ist eine geschickte Umsetzung des Gradientenabstiegs, bei der es vermieden wird Berechnungen mehrfach durchzuführen.
  • Welche Typen von Neuronalen Netzen gibt es?
    → Siehe Einordnung
  • Welche Aktivierungsfuktionen gibt es?
    → Siehe Übersicht
  • Welche Aktivierungsfunktionen machen bei einem einzelnen Perzeptron keinen Sinn?
    → Softmax wegen der Normierung; Maxout
  • Welche Aktivierungsfunktion macht in einem MLP keinen Sinn?
    → Nur lineare, da insgesamt eine lineare Funktion herauskommt.
  • Wofür kann man neuronale Netze einsetzen?
    → Klassifikation, Funktionsapproximation, Encoding, Dimensionalitätsreduktion, Assoziativspeicher
  • Welche Möglichkeiten zur Regularisierung gibt es?
    → L1, L2, Dropout, Weight Decay
  • Wie kann der Standard Gradient descent Algorithmus angepasst werden um den Lernvorgang zu beschleunigen?
    → Momentum, Exponential Decay Learning Rate, Performance Scheduling, Newbob, AdaGrad, RProp
  • Welche Alternativen zu standard Gradient Descent gibt es?
    → Quickprop, (L-)BFGS, Conjugate Gradient, Quasi-Newtonian (vgl. Reddit, Optimization Basics).
  • Wie kann man Netztopologien aufbauen?
    → Meiosis, Cascade Correlation, Optimal Brain Damage / Surgeon (vgl. Reddit).

Literatur

Vorlesungsempfehlungen

Folgende Vorlesungen sind ähnlich:

Übungsbetrieb

Übungsblätter sind freiwillig.

Termine und Klausurablauf

Datum: nach Terminvereinbarung
Ort: Gebäude 50.20
Übungsschein: gibt es nicht
Bonuspunkte: gibt es nicht
Erlaubte Hilfsmittel: keine

Published


by

Category

German posts

Tags

Contact